Trang chủ
Đề thi & kiểm tra
Lớp 12
Toán học
Bài tập Hàm số mức độ cơ bản, nâng cao cực hay có lời giải chi tiết !!
Cho hàm số y = f(x) = 1/ căn bậc...
Cho hàm số y = f(x) = 1/ căn bậc hai của(x^3 - 3x^2 + m -1)
Câu hỏi :
Cho hàm số y = f(x) = . Tìm tất cả các giá trị của m để đồ thị hàm số có 4 đường thẳng tiệm cận.
A. 1 < m < 5
B. -1 < m < 2
C. m < -1; m > 2
D. m < 1; m > 5
* Đáp án
A
* Hướng dẫn giải
Chọn A.
Ta có 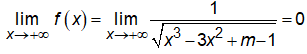
nên đồ thị hàm số có một đường tiệm cận ngang y = 0.
![]()
nên không tồn tại giới hạn
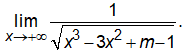
Do vậy đồ thị hàm số chỉ có một tiệm cận ngang y = 0.
Để đồ thị hàm số có bốn đường tiệm cận thì phương trình ![]() (1) có ba nghiệm phân biệt.
(1) có ba nghiệm phân biệt.
![]()
Số nghiệm của (2) là giao điểm của đường thẳng y = 1 –m và đồ thị hàm số ![]()
Xét hàm số ![]() Ta có
Ta có 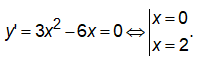
Bảng biến thiên
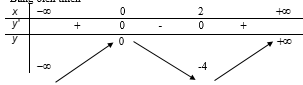
Dựa vào bảng biến thiên, ta thấy (2) có ba nghiệm phân biệt -4 < 1-m < 0 1 < m < 5
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập Hàm số mức độ cơ bản, nâng cao cực hay có lời giải chi tiết !!
Số câu hỏi: 236
Copyright © 2021 HOCTAP247
