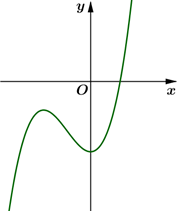
Cho hàm số y = ã^3 + bx^2 + cx + d có đồ thị là đường cong như hình vẽ bên.

Chọn B

Dựa vào đồ thị, ta có các nhận xét sau:

+ Ta thấy rằng $\underset{x\to -\infty }{\lim }y=-\infty ;\underset{x\to +\infty }{\lim }y=+\infty \Rightarrow a>0$.

+ Hàm số đạt cực đại tại $x_1<0,x_2=0$. Ta có $x_1,x_2$ là nghiệm phương trình $y^{\text{'}}=3a{x}^2+2bx+c=0$

Theo hệ thức Viét, ta có $\left\{\begin{array}{l}{x}_1+x_2=-\frac{2b}{3a}<0\\ x_1{x}_2=\frac{c}{3a}=0\end{array}\right.\iff \left\{\begin{array}{l}c=0\\ b>0\end{array}\right.$

+ Đồ thị hàm số đi qua điểm có tọa độ $\left(0;d\right)\Rightarrow d<0$.