Cho hình chóp S.ABC có SA vuông góc (ABC), AB = a căn bậc hai 3, góc ACB = 45 độ và

$SA=\frac{AB}{\tan \left(\widehat{ASB}\right)}=\frac{a\sqrt{3}}{\tan (60°)}=a$ 

$SB=\frac{AB}{\sin \left(\widehat{ASB}\right)}=\frac{a\sqrt{3}}{\sin (60°)}=2a$ 

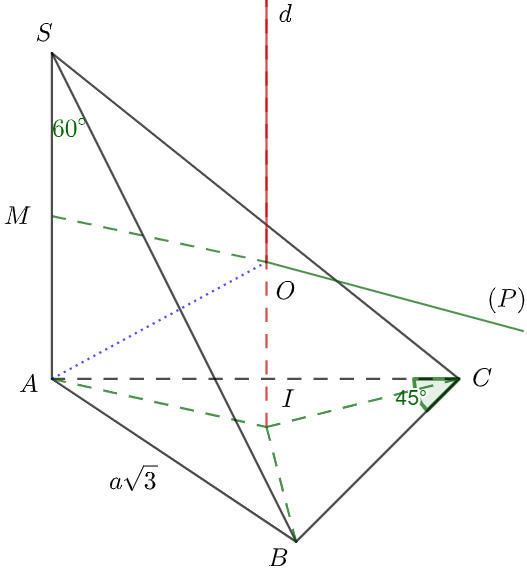
Gọi I là tâm đường tròn ngoại tiếp tam giác ABC

Áp dụng định lý sin ta có $\frac{AB}{\sin \left(\widehat{ACB}\right)}=\frac{a\sqrt{3}}{\sin (45°)}=a\sqrt{6}=2r$ 

$\iff r=\frac{a\sqrt{6}}{2}=IA$ 

Từ tâm I dựng đường thẳng d vuông góc với mặt đáy.

Lấy M là trung điểm của SA, tạo một mặt phẳng (P) qua M sao cho SA $\perp$ (P)

Mặt phẳng (P) cắt đường thẳng d tại một điểm O, đó là tâm mặt cầu cần tìm và độ dài AO chính là bán kính mặt cầu đó

Áp dụng định lý Pytago vào tam giác OAM vuông tại M

$AO=\sqrt{M{A}^2+O{M}^2}=\sqrt{\frac{1}{4}S{A}^2+A{I}^2}$ 

$=\sqrt{\frac{1}{4}{a}^2+{\left(\frac{a\sqrt{6}}{2}\right)}^2}=\frac{a\sqrt{7}}{2}$