Cho hình chóp S.ABC có tam giác SAC, tam giác ABC là những tam giác đều cạnh bằng a và (SAC) vuông góc

Đáp án đúng là: D

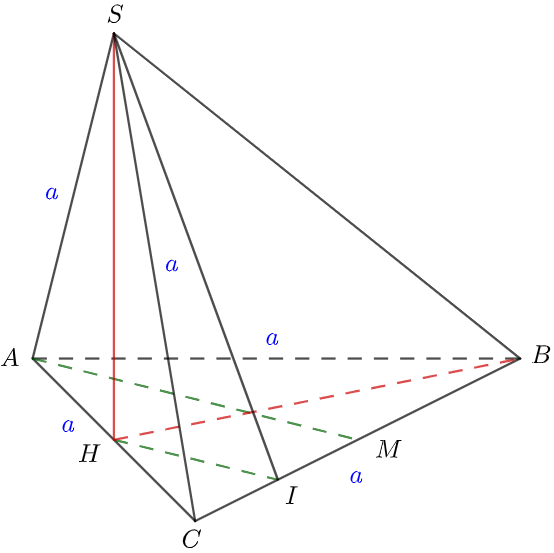
Lấy H là trung điểm của AC và tam giác ABC, tam giác SAC đều nên ta có SH $\perp$ AC, BH $\perp$AC

(SAC) $\perp$ (ABC)

Tam giác ABC đều nên với M là trung điểm của BC thì ta có AM $\perp$ BC

Kẻ HI // AM (I $\in$ BC) $\Rightarrow$ HI $\perp$ BC (*)

Kết hợp điều kiện SH $\perp$ BC (Do SH $\perp$ (ABC))

Nên suy ra BC $\perp$ (SHI) $\Rightarrow$ BC $\perp$ SI (**)

Từ (*) và (**) nên góc giữa hai mặt phẳng (ABC) và (SBC) chính là góc $\widehat{SIH}$ 

Xét tam giác SIH vuông tại H ta có $\tan \left(\alpha \right)=\tan \left(\widehat{SIH}\right)=\frac{SH}{HI}$ 

SH và AM là đường cao của tam giác đều có cạnh bằng a nên $SH=AM=\frac{a\sqrt{3}}{2}$ 

Từ đó suy ra $\tan \left(\alpha \right)=\frac{a\sqrt{3}}{2}:\frac{a\sqrt{3}}{4}=2$