Cho phương trình log2(x+1) +mlog (căn bậc 2 (x +1) 4) = 5 với tham số m.

* Hướng dẫn giải

Đáp án đúng là: D

Tập xác định

$\left\{\begin{array}{l}x+1>0\\ \sqrt{x+1}\ne 1\end{array}\right.\iff \left\{\begin{array}{l}x>-1\\ x\ne 0\end{array}\right.\iff x\in \in (-1;+\infty )\text{}\left\{\text{0}\right\}$ 

${\log }_2(x+1)+m{\log }_{\sqrt{x+1}}4=5$ 

$\iff {\log }_2(x+1)+m{\log }_{{(x+1)}^{\frac{1}{2}}}{2}^2=5$ 

$\iff {\log }_2(x+1)+2.\frac{1}{\frac{1}{2}}m{\log }_{x+1}2=5$ 

Đặt t = log₂ (x + 1) (t Î ℝ \ {0})

Phương trình (*) trở thành

$t+\frac{4m}{t}=5$ 

$\Rightarrow$ t² + 4m = 5t (Nhân 2 vế với t)

$\iff$ t² – 5t = –4m

Xét bảng biến thiên của f (t) = t² – 5t = –4m trên ℝ \ {0}

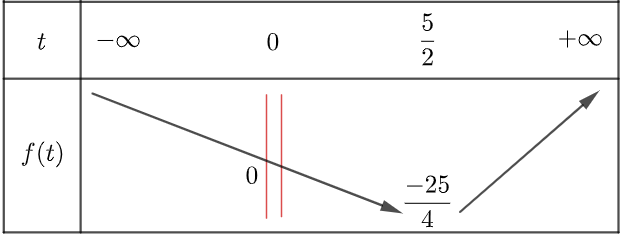
Dựa vào bảng biên thiên để phương trình có nghiệm thì $-4m\ge \frac{-25}{4}\iff m\le \frac{25}{16}$ 

Số giá trị nguyên dương của m là m = {1}