Cho biết hàm số f(x) = |x^2 -4x - 1 +m| có giá trị lớn nhất bằng 3 khi x thuộc [0; 3]. Số các giá trị của tham số

Đáp án đúng là: C

Xét hàm số g (x) = x² - 4x - 1 + m

$\Rightarrow g^{\text{'}}\left(x\right)=2x-4$ 

Ta có: $y\text{'}=f\text{'}\left(x\right)=\frac{g\text{'}\left(x\right).g\left(x\right)}{\left|g\left(x\right)\right|}=0$ 

$\Rightarrow [\begin{array}{c}g\text{'}\left(x\right)=0\\ g\left(x\right)=0\end{array}\iff [\begin{array}{c}2x-4=0\\ x^2-4x-1+m=0\end{array}$ 

$\iff [\begin{array}{c}x=2\\ x^2-4x-1+m=0\left(\text{*}\right)\end{array}$ 

+ TH1: Phương trình (*) không cho nghiệm mũ lẻ. Suy ra f (x) chỉ có một cực trị x = 2

Điều kiện: D = (-2)² - (-1 + m) = 5 - m $\le$0

$\iff$ m ³ 5

Ta xét bảng biến thiên của hàm số y = f (x) trên đoạn [0; 3]

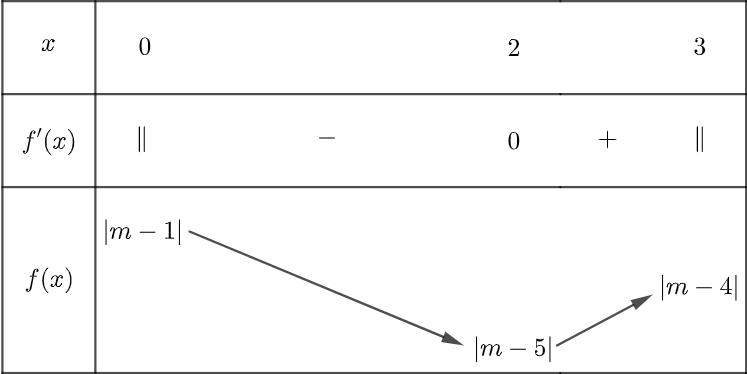
Với m ³ 5 $\Rightarrow |m-1|\ge |m-4|$ 

Vậy $ma{x}_{[0;3]}f\left(x\right)=|m-1|=m-1=3$ 

Û m = 4 (loại).

+ TH1: Phương trình (*) cho 2 nghiệm mũ lẻ. Suy ra f (x) chỉ có 3 cực trị x = 2, x = x₁ và x= x₂

Điều kiện: D = (-2)² - (-1 + m) = 5 - m > 0

$\iff$ m < 5

Ta xét bảng biến thiên của hàm số y = f (x) trên đoạn [0; 3]

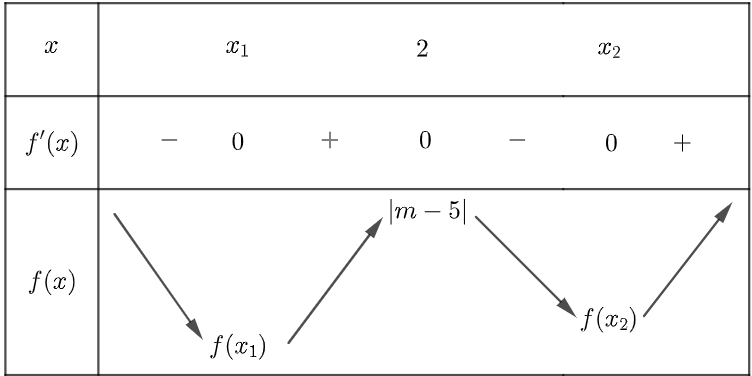
Với m < 5 nên f(2) > f (0) > f (3)

Kết hợp với dựa vào bảng biến thiên thì f (2) > f (x₁) và f (x₂)

Nên $ma{x}_{[0;3]}f\left(x\right)=|m-5|=5-m=3$ 

$\iff$ m = 2 (thỏa mãn)

Vậy chỉ có 1 giá trị của m thỏa mãn điều kiện bài toán là m = 2.