Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a căn 2, AD = a và AA' = a căn 3. Gọi M là trung điểm

* Hướng dẫn giải

Đáp án đúng là: C

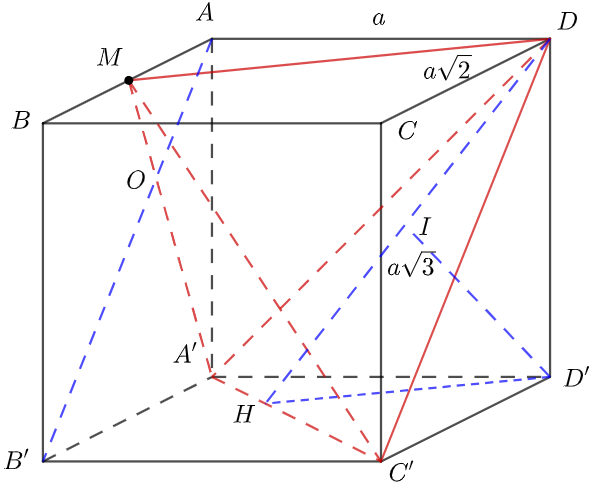
Áp dụng định lý Pytago ta có

$A\text{'}D=\sqrt{A\text{'}D{\text{'}}^2+DD{\text{'}}^2}=\sqrt{a^2+{\left(a\sqrt{3}\right)}^2}=2a$ 

$A\text{'}C\text{'}=\sqrt{A\text{'}D{\text{'}}^2+C\text{'}D{\text{'}}^2}=\sqrt{a^2+{\left(a\sqrt{2}\right)}^2}=a\sqrt{3}$ 

$DC\text{'}=\sqrt{DD{\text{'}}^2+C\text{'}D{\text{'}}^2}=\sqrt{{\left(a\sqrt{3}\right)}^2+{\left(a\sqrt{2}\right)}^2}=a\sqrt{5}$ 

Sử dụng công thức Hê-rông tính diện tích tam giác A’DC’

Ta có p là nửa chu vi tam giác A’DC’ với $p=\frac{A\text{'}D+DC\text{'}+C\text{'}A\text{'}}{2}$ 

$\Rightarrow p=\frac{2a+a\sqrt{5}+a\sqrt{3}}{2}=\left(\frac{2+\sqrt{5}+\sqrt{3}}{2}\right)a$  

Suy ra $S_{A\text{'}DC\text{'}}=\sqrt{p(p-A\text{'}D)(p-DC\text{'})(p-C\text{'}A\text{'})}$  (*)

Thay các giá trị vào (*) ta được $S_{A\text{'}DC\text{'}}=\frac{a^2\sqrt{11}}{2}$ 

Kẻ D’H $\perp$ A’C’ (H $\in$ A’C’)

D’I $\perp$DH (I $\in$ DH)

$\left.\begin{array}{r}DD\text{'}\perp A\text{'}C\text{'}\\ D\text{'}H\perp A\text{'}C\text{'}\end{array}\right\}\Rightarrow A\text{'}C\text{'}\perp (DD\text{'}H)$ 

Vậy khoảng cách từ D’ đến A’DC’ chính bằng ID’

Áp dụng hệ thức lượng trong tam giác vuông ta có

 $\frac{1}{ID{\text{'}}^2}=\frac{1}{DD{\text{'}}^2}+\frac{1}{HD{\text{'}}^2}=\frac{1}{DD{\text{'}}^2}+\frac{1}{A\text{'}D{\text{'}}^2}+\frac{1}{C\text{'}D{\text{'}}^2}$ 

$=\frac{1}{{\left(a\sqrt{3}\right)}^2}+\frac{1}{a^2}+\frac{1}{{\left(a\sqrt{2}\right)}^2}=\frac{11}{6a^2}$ 

$\Rightarrow ID\text{'}=\frac{a\sqrt{6}}{\sqrt{11}}$ 

Lại có, MA // A’B’ nên theo Ta-lét ta có

$\frac{MA}{A\text{'}B\text{'}}=\frac{OA}{OB}=\frac{MO}{OA\text{'}}=\frac{1}{2}\Rightarrow \frac{OA}{BA}=\frac{MO}{MA\text{'}}=\frac{1}{3}$ 

Kết hợp điều kiện AB’ // DC’

$\Rightarrow$2d_{M/(A’DC’)} = 3d_{O/(A’DC’)}

= 3d_{A/(A’DC’)} = 3d_{D’/(A’DC’)} = 3ID’

$\iff d_{M/(A’DC’)}=\frac{3}{2}ID\text{'}=\frac{3a\sqrt{6}}{2\sqrt{11}}$ 

Suy ra $V_{M.A\text{'}DC\text{'}}=\frac{1}{3}{d}_{M/(A\text{'}DC\text{'})}.S_{A\text{'}DC\text{'}}$ 

$=\frac{1}{3}.\frac{3a\sqrt{6}}{2\sqrt{11}}.\frac{a^2\sqrt{11}}{2}=\frac{a^3\sqrt{6}}{4}$