Trong mặt phẳng tọa độ Oxy, gọi A, B, C, D là 4 điểm cực trị của đồ thị hàm số y = |x|^3 - 6x^2 + 9|x| -3 với
Câu hỏi :
Trong mặt phẳng tọa độ Oxy, gọi A, B, C, D là 4 điểm cực trị của đồ thị hàm số với hoành độ đều khác 0. Bán kính đường tròn ngoại tiếp đi qua 4 điểm A, B, C, D bằng
Trong mặt phẳng tọa độ Oxy, gọi A, B, C, D là 4 điểm cực trị của đồ thị hàm số với hoành độ đều khác 0. Bán kính đường tròn ngoại tiếp đi qua 4 điểm A, B, C, D bằng
A.
B.
C.
D.
* Đáp án
* Hướng dẫn giải
Đáp án đúng là: C
+ Với x > 0 y = x3 - 6x2 + 9x - 3
(3x2 - 9x) - (3x - 9) = 0
3x.(x - 3) - 3(x - 3) = 0
3(x - 1).(x - 3) = 0
Suy ra xA = 1 thì tọa độ điểm A là (1; 1)
xB = 3 thì tọa độ điểm B là (3; -3)
+ Với x < 0 y = - x3 - 6x2 - 9x - 3
(- 3x2 - 9x) - (3x + 9) = 0
-3x.(x + 3) - 3(x + 3) = 0
-3(x + 1).(x + 3) = 0
Suy ra xC = -1 thì tọa độ điểm C là (-1; 1)
xD = 3 thì tọa độ điểm D là (-3; -3)
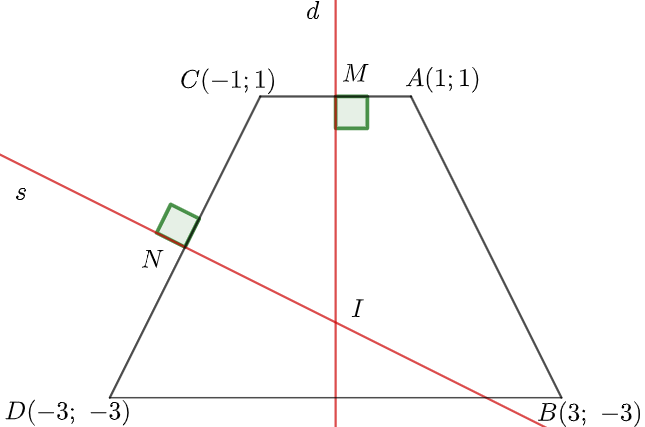
d là trục đối xứng của hình thang cân ABDC nên với mọi điểm nằm trên d luôn cách đều hai điểm A, C và hai điểm B, D (*)
Suy ra d là đường trung trực của hai đoạn thẳng AC và BD, cắt AC tại M
M là trung điểm của AC nên ta có tọa độ điểm M là M(xM; yM) với
Þ M(0; 1)
Kẻ đường thẳng s là đường trung trực của đoạn thẳng CD, cắt CD và d lần lượt tại N và I
Suy ra với mọi điểm trên s thì cách đều hai điểm C và D (**)
N là trung điểm của CD nên tương tự ta có tọa độ điểm N là N(-2; -1)
Từ (*) và (**) suy ra I là tâm đường tròn ngoại tiếp hình thang cân ABDC
Đường thẳng d đi qua M(0; 1) và có vectơ pháp tuyến là có phương trình (d): 2x = 0
I(0; yI)
Đường thẳng s đi qua N(-2; -1) và có vectơ pháp tuyến là có phương trình
2(x + 2) + 4(y+1) = 0
2x + 4 + 4y + 4 = 0
2x + 4y + 8 = 0
x + 2y + 4 = 0
Từ đây suy ra xI + 2yI + 4 = 0 Û yI = -2
Suy ra tọa độ điểm I là I(0; -2)
Vậy bán kính đường tròn ngoại tiếp ABDC là
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề kiểm tra Giữa học kì 2 Toán 12 có đáp án (Mới nhất) !!
Copyright © 2021 HOCTAP247
