Cho hình chóp S. ABC có đáy ABC là tam giác vuông, biết BA = BC = 2a, cạnh bên

Cách 1.

Ta có: BC ^ SA, BC ^ AB Þ BC ^ SB.

Ta có: $\widehat{SAC}=\widehat{SBC}$ = 90°.

Khi đó 4 điểm S, A, B, C nằm trên mặt cầu đường kính SC.

Bán kính mặt cầu R = $\frac{SC}{2}$ = 2a.

Diện tích mặt cầu ngoại tiếp hình chóp S = 4π(2a)² = 16πa².

Cách 2.

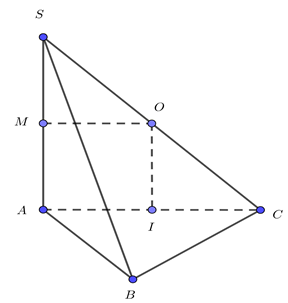
Gọi I là tâm đường tròn ngoại tiếp tam giác ABC, do tam giác ABC vuông tại B nên I là trung điểm của AC.

Qua I dựng đường thẳng d vuông góc với (ABC) nên ta được d // SA.

Trong tam giác SAC, dựng đường trung trực của SA cắt d tại O là tâm mặt cầu ngoại tiếp hình chóp S. ABC.

Ta tính được AC = 2a$\sqrt{2}$, SC = 4a.

Bán kính mặt cầu R = OA = $\sqrt{2a^2+2a^2}$ = 2a.

Diện tích mặt cầu ngoại tiếp hình chóp S.ABC là: