Trang chủ
Đề thi & kiểm tra
Lớp 12
Toán học
Đề kiểm tra Giữa học kì 2 Toán 12 có đáp án (Mới nhất) !!
Cho hàm số bậc ba y = f (x) có...
Cho hàm số bậc ba y = f (x) có đồ thị là đường cong (C) trong hình vẽ bên
Câu hỏi :
Cho hàm số bậc ba y = f (x) có đồ thị là đường cong (C) trong hình vẽ bên , biết hàm số f(x) đạt cực trị tại hai điểm x1 , x2 thỏa x2 = x1 + 4 và = −12. Gọi d là đường thẳng đi qua hai điểm cực trị của đồ thị (C). Diện tích hình phẳng giới hạn bởi (C) và d bằng
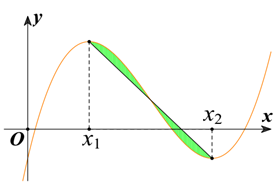

A. 8
B. 4
C. 2
D. 1
* Đáp án
* Hướng dẫn giải
Đáp án đúng là: A
Một hàm bậc ba nhận gốc tọa độ là điểm đối xứng thì y = ax3 + cx
Chọn x1 = −2 thì x2 = 2
Nên f(x) = x3 – 12x
Þ
Đường thẳng đi qua A(2; −16) và B(−2; 16) nhận = (−4; 32) = 4(−1; 8)
Þ d : −8(x – 2) – 1(y + 16) = 0 Û 8x + y = 0
Diện tích cần tìm là: 2S' = 2 = 2 . 4 = 8Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề kiểm tra Giữa học kì 2 Toán 12 có đáp án (Mới nhất) !!
Số câu hỏi: 444
Copyright © 2021 HOCTAP247
