Cho hình chóp S.ABC có đường cao SA tam giác ABC là tam giác

* Hướng dẫn giải

Phương pháp:

Xác định góc giữa các mặt phẳng (P) và (Q) ta thực hiện các bước sau:

+ Xác định giao tuyến d của (P) và (Q)

+ Trong mặt phẳng (P) xác định đường thẳng a$\perp$d trong mặt phẳng (Q) xác định đường thẳng b$\perp$d 

+ Khi đó góc giữa (P) và (Q) là góc giữa hai đường thẳng a và b

Cách giải:

Gọi M là trung điểm BC => AM$\perp$BC (do $∆$ABC cân tại A). 

Lại có $∆$SAB = $∆$SAC(c.g.c) hay $∆$SBC cân tại S

=> SM$\perp$BC

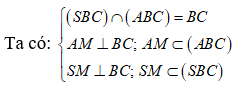
Theo đề bài

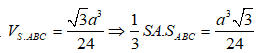
Lại thấy $∆$ABM vuông tại M có AB = a; 

Xét tam giác SAM vuông tại A có SA =  AM = $\frac{a}{2}$ nên $∆$SAM vuông cân tại A hay $\angle SMA= 45°$

Vậy góc giữa (SBC) và (ABC) bằng $45°$

Chọn D.