Trang chủ
Đề thi & kiểm tra
Lớp 12
Toán học
Đề kiểm tra Giữa học kì 2 Toán 12 có đáp án (Mới nhất) !!
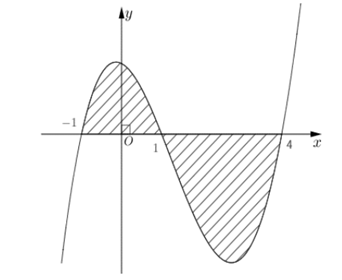
Cho hàm số f(x) liên tục tren R. Gọi V...
Cho hàm số f(x) liên tục tren R. Gọi V là thể tích hình phẳng giới hạn bởi các đường y = f(x), y = 0, x = −1 và x = 4
Câu hỏi :
Cho hàm số f(x) liên tục tren R. Gọi V là thể tích hình phẳng giới hạn bởi các đường y = f(x), y = 0, x = −1 và x = 4 (như hình vẽ bên) khi quay quanh trục Ox. Mệnh đề nào sau đây sai?

A. V =
B. V =
C. V =
D. V =
* Đáp án
* Hướng dẫn giải
Đáp án đúng là: A
Ta có: hàm số f(x) ≥ 0 ∀ x ∈ [−1; 1]; f(x) ≤ 0 ∀ x ∈ [1; 4], nên ta có:
Vậy thể tích hình phẳng giới hạn bởi các đường y = f(x), y = 0, x = −1 và x = 4 là:
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề kiểm tra Giữa học kì 2 Toán 12 có đáp án (Mới nhất) !!
Số câu hỏi: 444
Copyright © 2021 HOCTAP247
