Cho hình chóp S.ABCD có đáy là hình bình hành và SA = SB = SC

* Hướng dẫn giải

Đáp án là D

Do SB = SC = 11 và  do đó BC = 11

Ta lại có, SA = SC = 11 và  vuông cân tại S hay AC = 11$\sqrt{2}$

Mặt khác, SA = SB = 11 và 

Từ đó, ta có  suy  ra $∆$ABC vuông tại C

Gọi H là trung điểm của AB Khi đó, H là tâm đường tròn ngoại tiếp $∆$ABC. Vì SA = SB = SC nên SH$\perp$(ABC)

Gọi M là điểm trên CD sao cho HM$\perp$AB suy ra HM$\perp$CD. Gọi N là chân đường vuông góc hạ từ C xuống AB. Khi đó, HM//CN và HM = CN. Do $∆$ABC vuông tại C nên theo công thức tính diện tích ta có:

Ta lại có, 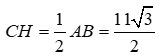 nên 

Trong tam giác vuông SHM dựng đường cao HI(I$\in$SM) suy ra HI$\perp$(SCD). Khi đó,