y = x3 + 3x (C). Gọi (d) là tiếp tuyến của (C) tại điểm M (1; 4). Tính diện tích hình phẳng

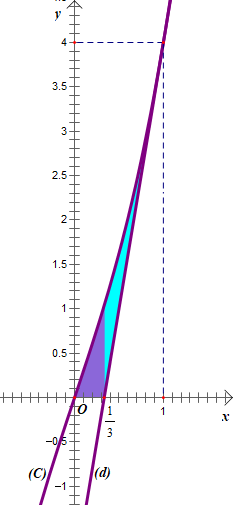
Phương trình hoành độ giao điểm của (C) và trục hoành là:

x³ + 3x = 0 Û $\left[\begin{array}{l}x=0\\ x^2=-3\left(vl\right)\end{array}\right.$

Û x = 0

Phương trình hoành độ giao điểm của (d) và trục hoành là:

6x – 2 = 0 Û x = $\frac{1}{3}$

Do đó diện tích hình phẳng giới hạn bởi (C), (d) và trục hoành là:

S = $\underset{0}{\overset{\frac{1}{3}}{\int }}\left(x^3+3x\right)$ + $\underset{\frac{1}{3}}{\overset{1}{\int }}\left(x^3+3x-6x+2\right)d\text{x}$

S = $\underset{0}{\overset{\frac{1}{3}}{\int }}\left(x^3+3x\right)$ + $\underset{\frac{1}{3}}{\overset{1}{\int }}\left(x^3-3x+2\right)d\text{x}$

$={\left.\left(\frac{x^4}{4}+\frac{3}{2}{x}^2\right)\right|}_0^{\frac{1}{3}}+{\left.\left(\frac{x^4}{4}-\frac{3}{2}{x}^2+2x\right)\right|}_{\frac{1}{3}}^1$

$=\left[\frac{{\left(\frac{1}{3}\right)}^4}{4}+\frac{3}{2}.{\left(\frac{1}{3}\right)}^2\right]+\left[\frac{1^4}{4}-\frac{3}{2}{.1}^2+2.1-\frac{{\left(\frac{1}{3}\right)}^4}{4}+\frac{3}{2}.{\left(\frac{1}{3}\right)}^2-2.\frac{1}{3}\right]$

$=\frac{1}{81.4}+\frac{3}{2}.\frac{1}{9}+\frac{1}{4}-\frac{3}{2}+2-\frac{1}{81.4}+\frac{3}{2}.\frac{1}{9}-\frac{2}{3}$

$=\frac{1}{6}+\frac{1}{4}-\frac{3}{2}+2+\frac{1}{6}-\frac{2}{3}$

$=\frac{5}{12}$

Vậy ta chọn phương án A.