Trong không gian với hệ tọa độ Oxyz, cho hai điểm M(−2; −2; 1), A(1; 2; −3) và đường thẳng d

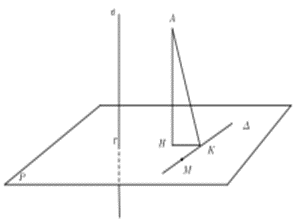
Gọi (P) là mặt phẳng đi qua M và vuông góc với d, khi đó (P) chứa ∆

Mặt phẳng (P) qua M(−2; −2; 1) và có vectơ pháp tuyến $\overrightarrow{n_P}$ = $\overrightarrow{u_d}$ = (2; 2; −1) nên có phương trình : (P) : 2x + 2y – z + 9 = 0

Gọi H, K lần lượt là hình chiếu của A lên (P) và ∆. Khi đó: AK ≥ AH nên AK min khi

K ≡ H. Đường thẳng AH đi qua A(1; 2; −3) và có vectơ chỉ phương $\overrightarrow{u_d}$ = (2; 2; −1) nên AH có phương trình tham số:

$\left\{\begin{array}{c}x=1+2t\\ y=2+2t\\ z=-3-t\end{array}\right.$  

H ∈ AH Þ H(1 + 2t; 2 + 2t; −3 – t)

H ∈ (P) Þ 2(1 + 2t) + 2(2 + 2t) –(−3 – t) + 9 = 0 Þ H(−3; −2; −1)

Nên $\overrightarrow{u}$ = $\overrightarrow{HM}$ = (1; 0; 2)

Vậy a = 0; b = 2 Þ a + 2b = 4