Trong không gian Oxyz, cho hai điểm A(3; -2; 6), B(0; 1; 0) và mặt cầu (S): (x - 1)^2 + (y - 2)^2 + (z - 3)^2 = 25.
Câu hỏi :
Trong không gian Oxyz, cho hai điểm A(3; -2; 6), B(0; 1; 0) và mặt cầu (S): (x - 1)2 + (y - 2)2 + (z - 3)2 = 25. Mặt phẳng (P): ax + by + cz - 2 = 0 đi qua A, B và cắt mặt cầu (S) theo giao tuyến là đường tròn có bán kính nhỏ nhất. Biểu thức T = a + b + c có giá trị bằng
Trong không gian Oxyz, cho hai điểm A(3; -2; 6), B(0; 1; 0) và mặt cầu (S): (x - 1)2 + (y - 2)2 + (z - 3)2 = 25. Mặt phẳng (P): ax + by + cz - 2 = 0 đi qua A, B và cắt mặt cầu (S) theo giao tuyến là đường tròn có bán kính nhỏ nhất. Biểu thức T = a + b + c có giá trị bằng
A. 3;
B. 5;
C. 2;
* Đáp án
* Hướng dẫn giải
Đáp án đúng là: A
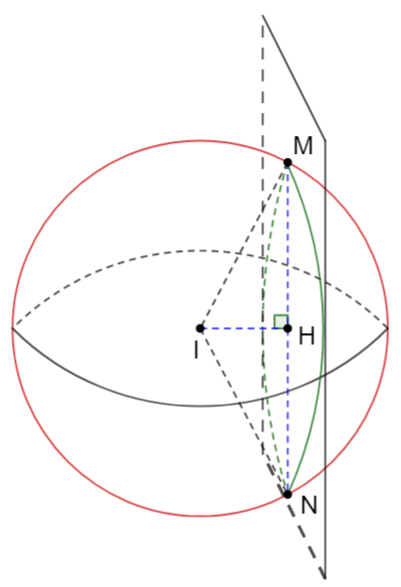
Mặt cầu (S): (x - 1)2 + (y - 2)2 + (z - 3)2 = 25 có tâm I(1; 2; 3) và bán kính R = 5
Mặt phẳng (P): ax + by + cz - 2 = 0 đi qua A, B nên ta có hệ phương trình
Từ đó mặt phẳng (P) trở thành
(P): (2 - 2c)x + 2y + cz - 2 = 0
Để mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn có bán kính nhỏ nhất
thì khoảng cách từ I đến mặt phẳng (P) là lớn nhất
+) Xét c = 0
+) Xét c ¹ 0 nên ta có
Xét hàm số trên ℝ ta thấy f (x) đạt GTLN là khi và chỉ khi t = 1
(Thỏa mãn )
Từ đó a = 2 - 2.1 = 0
Vậy khi đó T = a + b + c = 0 + 2 + 1 = 3.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề kiểm tra Học kì 2 Toán 12 có đáp án (Mới nhất) !!
Copyright © 2021 HOCTAP247
