Trang chủ
Đề thi & kiểm tra
Lớp 12
Toán học
333 Bài trắc nghiệm Hình học Khối đa diện cực hay có lời giải chi tiết !!
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a,...
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, BC
Câu hỏi :
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, BC = 2a, AC' = a. Điểm N thuộc cạnh BB’ sao cho BN = 2NB', điểm M thuộc cạnh DD’ sao cho D'M = 2MD. Mp(A'MN) chia hình hộp chữ nhật làm hai phần, tính thể tích phần chứa điểm C'.
A. 4
B.
C. 2
D. 3
* Đáp án
* Hướng dẫn giải
Đáp án là C
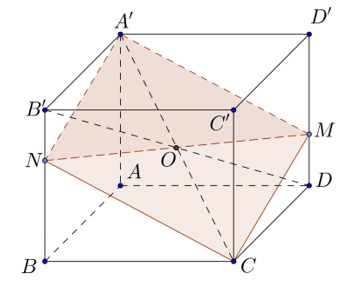
Nhận xét: B'NDM là hình bình hành (B'N = DM, B'N//DM)
=> MNB'D = O là trung điểm của mỗi đoạn nên O cũng là trung điểm của đường chéo A'C.
Vậy thiết diện tạo bởi mặt (A'MN) và hình chóp là hình bình hành A'NCM.
Ta có: ![]()
Cách 1:
Thể tích phần chứa C' là
![]()
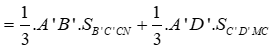
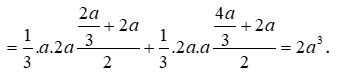
Cách 2: Áp dụng công thức tính nhanh
Gọi thể tích phần chứa C' là V'.
Ta có: 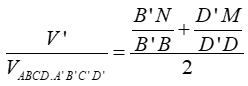
![]()
Cách 3: Nhận xét nhanh do đa diện chứa C' đối xứng với đa diện không chứa C' qua O nên thể tích của hai phần này bằng nhau, suy ra 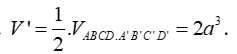
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
333 Bài trắc nghiệm Hình học Khối đa diện cực hay có lời giải chi tiết !!
Số câu hỏi: 326
Copyright © 2021 HOCTAP247
