Trang chủ
Đề thi & kiểm tra
Lớp 12
Toán học
Đề kiểm tra Học kì 2 Toán 12 có đáp án (Mới nhất) !!
Cho hàm số y = f (x) có đạo hàm...
Cho hàm số y = f (x) có đạo hàm liên tục trên ℝ và có bảng biến thiên như dưới đây. Có tất cả bao nhiêu
Câu hỏi :
Cho hàm số y = f (x) có đạo hàm liên tục trên ℝ và có bảng biến thiên như dưới đây
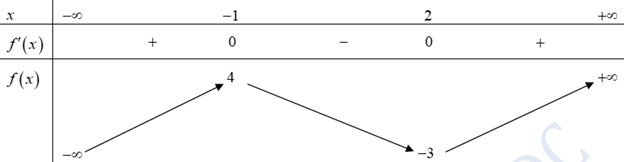
Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-2022; 2022] để hàm số g (x) = f 3(x) - mf (x) có nhiều điểm cực trị nhất?
Cho hàm số y = f (x) có đạo hàm liên tục trên ℝ và có bảng biến thiên như dưới đây

Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-2022; 2022] để hàm số g (x) = f 3(x) - mf (x) có nhiều điểm cực trị nhất?
A. 26;
B. 27;
C. 2022;
D. 2021.
* Đáp án
* Hướng dẫn giải
Đáp án đúng là: A
g (x) = f 3(x) - mf (x)
Þ g '(x) = 3f '(x).f 2(x) - mf '(x) = 0
Để có nhiều cực trị nhất thì m > 0
+) TH1: f '(x) = 0 Þ x = -1, x = 2
+) TH2: (1)
Để hàm số g (x) = f 3(x) - mf (x) có nhiều điểm cực trị nhất thì phương trình
cho 3 nghiệm phân biệt
+) TH2: (1)
Để hàm số g (x) = f3 (x) - mf (x) có nhiều điểm cực trị nhất thì phương trình
cho 3 nghiệm phân biệt
Vậy suy ra 0 < m < 27
Vậy có 26 giá trị của m thỏa mãn.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề kiểm tra Học kì 2 Toán 12 có đáp án (Mới nhất) !!
Số câu hỏi: 713
Copyright © 2021 HOCTAP247
