Cho khối chóp S.ABC có SA = a căn 2, SB = 2a, SC = 2 căn 2 a

* Hướng dẫn giải

Chọn D.

Gọi là hình chiếu vuông góc của A lên mp (SBC) . Gọi I, K lần lượt là hình chiếu vuông góc của H lên SB và SC.

Ta có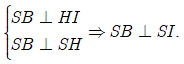 

Chứng minh tương tự ta được SC$\perp$SK

$∆$SAI = $∆$SAK  (cạnh huyền – góc nhọn) => SI = SK

Khi đó $∆$SHI = $∆$SHK  (cạnh huyền – cạnh góc vuông) => HI = HK. Do đó SH là đường phan giác trong của BSC, nên HSI = 30$°$

Trong tam giác vuông SAI, 

Trong tam giác vuông HIS, 

Khi đó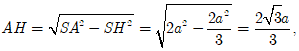 

Vậy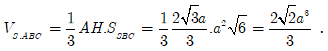 

Cách 2: Sử dụng công thức tính nhanh

Nếu khối chóp S.ABC có 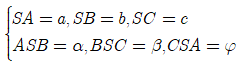 thì 

Áp dụng: Với 

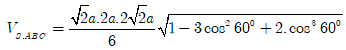
Cách 3:

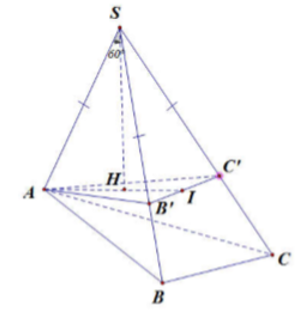
Trên các cạnh SB, SC lần lượt lấy các điểm B’, C’ sao cho SB' = SC' = SA = a$\sqrt{2}$

Khi đó chóp S.AB'C' là khối chóp tam giác đều. Đồng thời ASB = BSC = CSA = 60$°$ nên AB' = B'C' = AC' = SA = a$\sqrt{2}$

Gọi H là hình chiếu của S lên mặt phẳng (AB'C'). Khi đó dễ dàng chứng minh được các tam giác SHA, SHB', SHC' bằng nhau. Suy ra HA, HB', HC' bằng nhau. Hay H là tâm đường tròn ngoại tiếp tam giác AB'C'. Vì tam giác AB'C' đều nên H cũng là trọng tâm tam giác AB'C'.

Ta có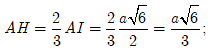 

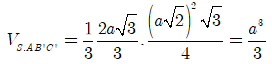
Ta có