Trang chủ
Đề thi & kiểm tra
Lớp 12
Toán học
Đề kiểm tra Học kì 2 Toán 12 có đáp án (Mới nhất) !!
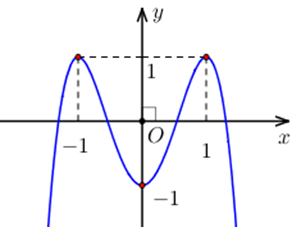
Cho hàm số bậc bốn y = f (x) có...
Cho hàm số bậc bốn y = f (x) có đồ thị là đường cong trong hình bên. Phương trình f (f (x) - 1) = 0
Câu hỏi :
Cho hàm số bậc bốn y = f (x) có đồ thị là đường cong trong hình bên. Phương trình f (f (x) - 1) = 0 có ít nhất bao nhiêu nghiệm?

A. 4;
B. 8;
C. 6;
D. 12.
* Đáp án
* Hướng dẫn giải
Đáp án đúng là: B
Dựa vào đồ thị hàm số ta thấy
f (f (x) - 1) = 0
+) TH1: f (x) - 1 = a Û f (x) = a + 1 (-1 < a + 1 < 0)
Phương trình cho ít nhất 4 nghiệm phân biệt
+) TH2: f (x) - 1 = b Û f (x) = b + 1 (0 < b + 1 < 1)
Phương trình cho 4 nghiệm phân biệt
+) TH3: f (x) - 1 = c Û f (x) = c + 1 (1 < c + 1 < 2)
Phương trình vô nghiệm
+) TH4: f (x) - 1 = d Û f (x) = d + 1 (2 < d + 1 < 3)
Phương trình vô nghiệm
Vậy suy ra phương tình f (f (x) - 1) = 0 cho ít nhất 8 nghiệm phân biệt.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề kiểm tra Học kì 2 Toán 12 có đáp án (Mới nhất) !!
Số câu hỏi: 713
Copyright © 2021 HOCTAP247
