Trong không gian Oxyz, cho mặt cầu (S): x^2 + y^2 + z^2 + 2x - 4y + 2z - 3 = 0. Viết phương trình
Câu hỏi :
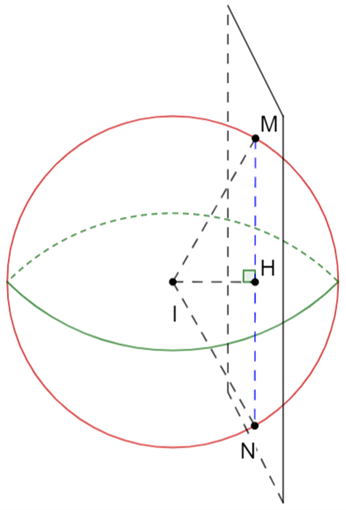
Trong không gian Oxyz, cho mặt cầu (S): x2 + y2 + z2 + 2x - 4y + 2z - 3 = 0. Viết phương trình mặt phẳng (a) chứa trục Oz cắt mặt cầu (S) theo thiết diện là đường tròn có chu vi bằng 6p.
Trong không gian Oxyz, cho mặt cầu (S): x2 + y2 + z2 + 2x - 4y + 2z - 3 = 0. Viết phương trình mặt phẳng (a) chứa trục Oz cắt mặt cầu (S) theo thiết diện là đường tròn có chu vi bằng 6p.
A. 2y + z = 0;
B. 2x + y = 0;
C. 2x - y = 0;
* Đáp án
* Hướng dẫn giải
Đáp án đúng là: B
(S): x2 + y2 + z2 + 2x - 4y + 2z - 3 = 0
Û (x2 + 2x + 1) + (y2 - 4y + 4) + (z2 + 2z +1) = 9
Û (x + 1)2 + (y - 2)2 + (z + 1)2 = 9
Vậy mặt cầu (S) có tâm là điểm I(-1; 2; -1) và R = 3
Phương trình mặt phẳng (a) chứa trục Oz cắt mặt cầu (S) theo thiết diện là đường tròn có bán kính là HM
Nên suy ra C = 2p.HM = 6p Þ HM = 3 = R
Vậy mặt phẳng đã cho đi qua tâm I của mặt cầu
Phương trình mặt phẳng (a) chứa trục Oz nên véc-tơ pháp tuyến của (a) là vuông góc với véc-tơ chỉ phương của Oz là (0; 0; 1)
Þ a.0 + b.0 + c.1 = 0
Þ c = 0
Vậy phương trình mặt phẳng (a) đi qua I và có véc-tơ pháp tuyến là
a.(x + 1) + b.(y -2) = 0
Û ax + by + (a - 2b) = 0 (1)
Do phương trình mặt phẳng (a) đi qua Oz nên đi qua điểm O
Vậy từ (1) ta có a - 2b = 0 Û a = 2b
Thay a = 2b vào (1) nên suy ra (1) trở thành
2bx + by = 0
Û 2x + y = 0.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề kiểm tra Học kì 2 Toán 12 có đáp án (Mới nhất) !!
Copyright © 2021 HOCTAP247
