Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): (x - 1)^2 + (y + 2)^2 + (z - 3)^2 = 12. Gọi (P) là mặt phẳng
Câu hỏi :
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): (x - 1)2 + (y + 2)2 + (z - 3)2 = 12. Gọi (P) là mặt phẳng đi qua hai điểm và cắt mặt cầu (S) theo giao tuyến là đường tròn (C) sao cho khối nón có đỉnh là tâm của (S), đáy là hình tròn (C) có thể tích lớn nhất. Biết mặt phẳng (P) có phương trình dạng 2x + by + cz + d = 0. Khi đó giá trị biểu thức b2 + c2 + d2 bằng
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): (x - 1)2 + (y + 2)2 + (z - 3)2 = 12. Gọi (P) là mặt phẳng đi qua hai điểm và cắt mặt cầu (S) theo giao tuyến là đường tròn (C) sao cho khối nón có đỉnh là tâm của (S), đáy là hình tròn (C) có thể tích lớn nhất. Biết mặt phẳng (P) có phương trình dạng 2x + by + cz + d = 0. Khi đó giá trị biểu thức b2 + c2 + d2 bằng
A. 144;
B. 113;
C. 105;
* Đáp án
* Hướng dẫn giải
Đáp án đúng là: D
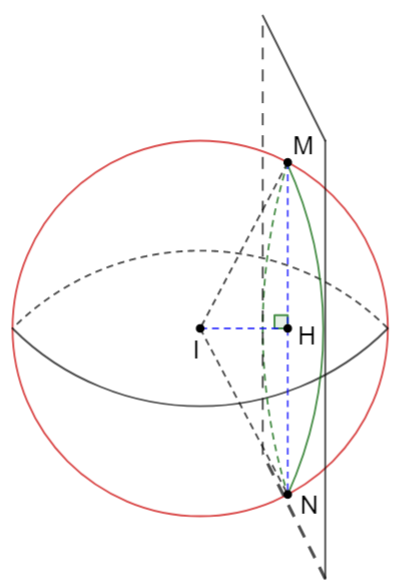
Mặt cầu (S): (x - 1)2 + (y + 2)2 + (z - 3)2 = 12 có tâm I(1; -2; 3) và bán kính
+)
+) Mặt phẳng (P) có phương trình dạng 2x + by + cz + d = 0 có véc-tơ pháp tuyến là
AB thuộc mặt phẳng (P) nên véc-tơ pháp tuyến của (P) vuông góc với
Ta suy ra được hệ phương trình
Từ đó suy ra (P) có dạng 2x + by - z + 11 = 0
Khối nón có đỉnh là tâm của (S), đáy là hình tròn (C) có thể tích là
đạt GTLN khi IH(12 - IH2) đạt GTLN
Ta có:
Với x > 0, xét hàm số f (x) = x(12 - x2) = 12x - x3
Þ f '(x) = 12 - 3x2 = 0 Û x2 = 4 Þ x = 2 (Do x > 0)
Vẽ được BBT của hàm số f (x) = x(12 - x2) trên (0; +¥)
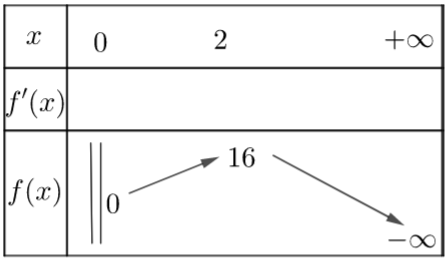
Dựa vào BBT nên suy ra f (x) đạt GTLN bằng 16 khi x = 2
Nên suy ra IH(12 - IH2) đạt GTLN khi IH = 2
Þ |5 - b|2 = b2 + 5
Û 25 - 10b + b2 = b2 + 5
Û 10b = 20 Û b = 2
Từ đó suy ra b2 + c2 + d2 = 22 + (-1)2 + 112 = 126.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề kiểm tra Học kì 2 Toán 12 có đáp án (Mới nhất) !!
Copyright © 2021 HOCTAP247
