Cho hai số phức z1, z2, thỏa mãn |z1 + 6| = 5, |z2 + 2 - 3i| = |z2 - 2 - 6i|. Giá trị nhỏ nhất của |z1 - z2| bằng

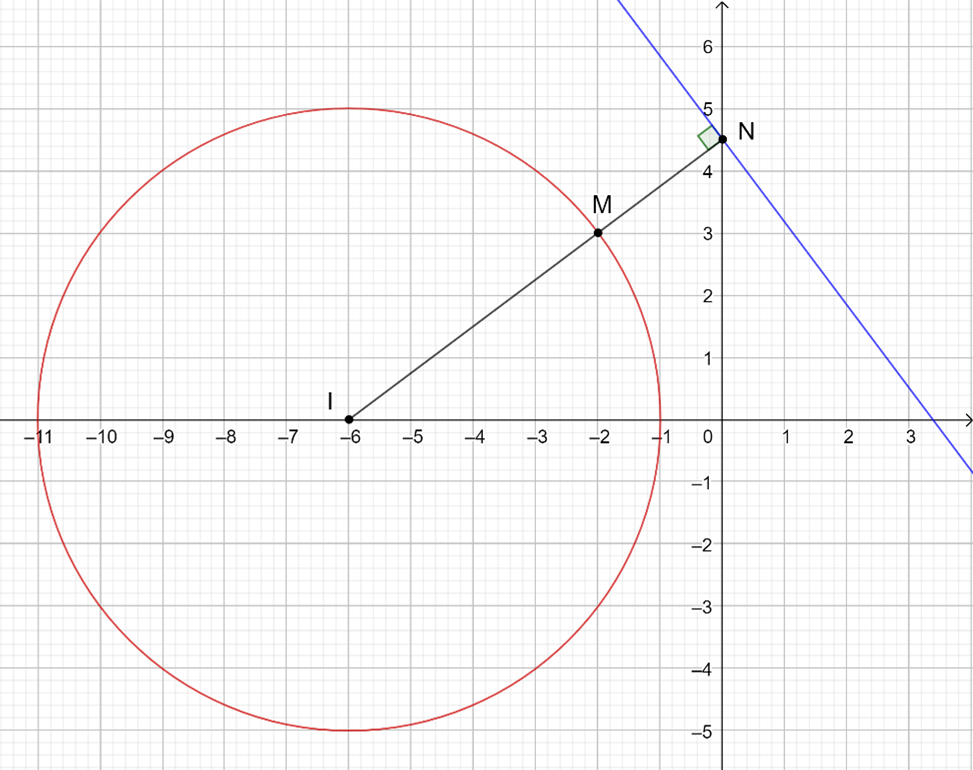
+) |z₁ + 6| = 5

Û (x₁ + 6)² + y₁² = 25

M(x₁; y₁) là điểm biểu diễn của số phức z₁ và thuộc đường tròn tâm I(-6; 0) có bán kính R = 5

+) |z₂ + 2 - 3i| = |z₂ - 2 - 6i|

Û (x₂ + 2)² + (y₂ - 3)² = (x₂ - 2)² + (y₂ - 6)²

Û x₂² + 4x₂ + 4 + y₂² - 6y₂ + 9 = x₂² - 4x₂ + 4 + y₂² - 12y₂ + 36

Û 8x₂ + 6y₂ - 27 = 0

N(x₂; y₂) là điểm biểu diễn của số phức z₂ và thuộc đường thẳng 8x + 6y - 27 = 0

Ta có |z₁ - z₂| bằng MN và để |z₁ - z₂| đạt GTNN thì MN nhỏ nhất

Khi đó đường thẳng MN đi qua I, vuông góc với đường thẳng trên và M gần N nhất

Theo hình vẽ

MN_min = IN - IM