Trang chủ
Đề thi & kiểm tra
Lớp 12
Toán học
333 Bài trắc nghiệm Hình học Khối đa diện cực hay có lời giải chi tiết !!
Cho hình tứ diện ABCD có tất cả các cạnh...
Cho hình tứ diện ABCD có tất cả các cạnh bằng 6a. Gọi M, N
Câu hỏi :
Cho hình tứ diện ABCD có tất cả các cạnh bằng 6a. Gọi M, N lần lượt là trung điểm của CA, CB. P là điểm trên cạnh BD sao cho BP = 2PD. Diện tích S thiết diện của tứ diện ABCD bị cắt bởi (MNP) là
A. S =
B. S =
C. S =
D. S =
* Đáp án
D
* Hướng dẫn giải
Chọn D.
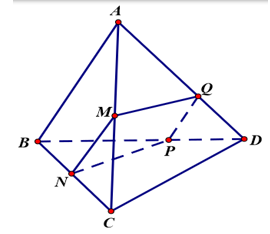
Trong mặt phẳng (ABD) qua P kẻ đường thẳng song song AB cắt AD tại Q, ta có
![]()
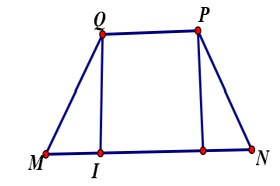
Dễ thấy MN là đường trung bình của tam giác ABC nên MN//AB//PQ, nên 4 điểm M, N, P, Q đồng phẳng MNPQ và MN = 3a, thiết diện cần tìm chính là hình thang MNPQ là hình thang cân, ta có
![]()
![]()
Kẻ đường cao QI ta có:
![]()
![]()
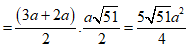
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
333 Bài trắc nghiệm Hình học Khối đa diện cực hay có lời giải chi tiết !!
Số câu hỏi: 326
Copyright © 2021 HOCTAP247
