Trang chủ
Đề thi & kiểm tra
Lớp 12
Toán học
333 Bài trắc nghiệm Hình học Khối đa diện cực hay có lời giải chi tiết !!
Cho hình chóp S.ABC có đáy là tam giác vuông...
Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B, AC
Câu hỏi :
Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B, AC = a, biết SA vuông góc với mặt đáy, SA = a. Gọi G là trọng tâm của tam giác SBC, là mặt phẳng đi qua AG và song song với BC cắt SB, SC lần lượt tại M và N. Tính thể tích V của khối đa diện AMNBC.
A. V =
B. V =
C. V =
D. V =
* Đáp án
D
* Hướng dẫn giải
Chọn D.
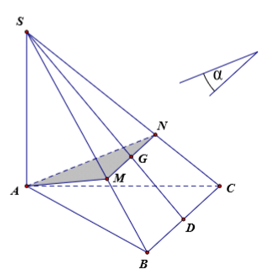
Do () đi qua G(SBC), song song với BC nên () cắt mặt phẳng (SBC) theo giao tuyến MN qua G và song song với BC.
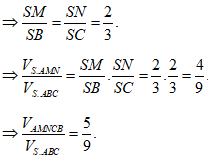
Do tam giác ABC vuông cân tại B, AC = a nên ![]()
Do SA(ABC) nên ![]()
![]()
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
333 Bài trắc nghiệm Hình học Khối đa diện cực hay có lời giải chi tiết !!
Số câu hỏi: 326
Copyright © 2021 HOCTAP247
