Cho hình chóp có đáy là hình vuông tâm O, cạnh bằng 4a. Cạnh bên

* Hướng dẫn giải

Phương pháp:

Sử dụng lí thuyết d(a,b) = d(a,(P)) = d(A,(P)), ở đó a,b chéo nhau, (P) chứa b và song song a và A$\in$a để tìm khoảng cách giữa hai đường thẳng SD, AB.

Tính khoảng cách và kết luận.

Cách giải:

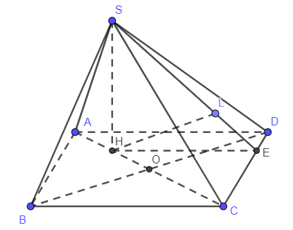
Do AB//CD nên

Kẻ 

Ta có: SA = 2a, 

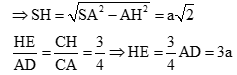
Khi đó