Trang chủ
Đề thi & kiểm tra
Lớp 12
Toán học
Đề trắc nghiệm Chương 3 Giải tích 12 Trường THPT TX Quảng Trị năm học 2018 - 2019
Cho hàm số \(y=f(x)\) có đạo hàm liên tục trên...
Cho hàm số \(y=f(x)\) có đạo hàm liên tục trên [- 2;4]. Đồ thị của hàm số \(y=f(x)\) được cho như hình bên.
Câu hỏi :
Cho hàm số \(y=f(x)\) có đạo hàm liên tục trên [- 2;4]. Đồ thị của hàm số \(y=f'(x)\) được cho như hình bên. Diện tích hình phẳng giới hạn bởi trục Ox và đồ thị hàm số \(y=f'(x)\) trên đoạn [-2;1] và [1;4] lần lượt bằng 9 và 12. Cho \(f(1)=3\). Tính tổng \(f\left( { - 2} \right) + f\left( 4 \right).\)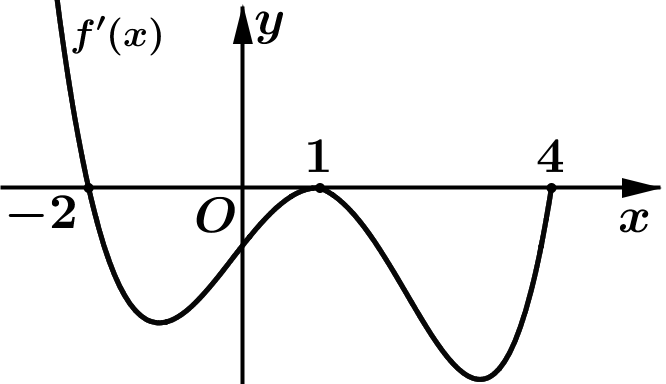
* Đáp án
* Hướng dẫn giải
Theo giả thiết, ta có \(\int\limits_{ - 2}^1 {f'\left( x \right){\rm{d}}x} = - 9\) và \(\int\limits_1^4 {f'\left( x \right){\rm{d}}x} = - 12.\)
• \(\int\limits_{ - 2}^1 {f'\left( x \right){\rm{d}}x} = - 9 \Leftrightarrow f\left( 1 \right) - f\left( { - 2} \right) = - 9 \Leftrightarrow 3 - f\left( { - 2} \right) = - 9f\left( { - 2} \right) = 12.\)
• \(\int\limits_1^4 {f'\left( x \right){\rm{d}}x} = - 12 \Leftrightarrow f\left( 4 \right) - f\left( 1 \right) = - 12 \Leftrightarrow f\left( 4 \right) - 3 = - 12f\left( 4 \right) = - 9.\)
Vậy \(f\left( { - 2} \right) + f\left( 4 \right) = 12 + \left( { - 9} \right) = 3.\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề trắc nghiệm Chương 3 Giải tích 12 Trường THPT TX Quảng Trị năm học 2018 - 2019
Số câu hỏi: 25
Copyright © 2021 HOCTAP247
