Cho hàm số f(x) = (x-1)^2 (ax^2 + 4ax -a + b - 2) với a,b thuộc

* Hướng dẫn giải

Chọn C

Tập xác định của hàm số là $\mathrm{ℝ}$ .

Ta có: 

Vì trên khoảng $\left(-\frac{4}{3};0\right)$ hàm số đạt giá trị lớn nhất tại x = -1 nên hàm số đạt cực trị tại x = -1( cũng là điểm cực đại của hàm số) và a > 0.

Khi đó f'(x) = 0 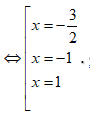( đều là các nghiệm đơn)

Hàm số đạt cực đại tại x = -1 nên có bảng biến thiên:

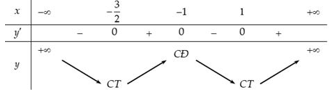
=> x = $-\frac{3}{2}$là điểm cực tiểu duy nhất thuộc $\left[-2;-\frac{5}{4}\right]$ 

Vậy hàm số đạt giá trị nhỏ nhất tại x = $-\frac{3}{2}$ trên đoạn $\left[-2;-\frac{5}{4}\right]$