Gọi S là tập hợp các giá trị của m để hàm số y = |x^3 - 3x^2

* Hướng dẫn giải

Chọn A

Xét hàm số g(x) = $x^3-3x^2+m$ có  Xét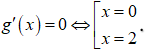 

Khi đó giá trị lớn nhất của hàm số y = |$x^3-3x^2+m$| trên [-2;4] là:

Trường hợp 1: Giả sử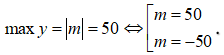 

Với m = 50 thì |m + 16| = 66 > 50 (loại)

Với m = -50 thì |m - 20| = 70 > 50 (loại)

Trường hợp 2: Giả sử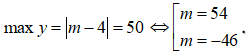 

Với m = 54 => |m| = 54 > 50 (loại)

Với m = -46 thì |m - 20| = 66 > 50 (loại)

Trường hợp 3: Giả sử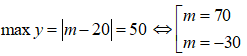 

Với m = 70 thì |m + 16| = 86 > 50 (loại)

Với m = -30 thì |m + 16| = 14 < 50,  (thỏa mãn)

Trường hợp 4: Giả sử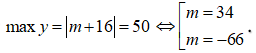 

Với m = 34 thì |m| = 34 < 50,  (thỏa mãn)

Với m = -66 thì |m| = 66 > 50 (loại)

Vậy  Do đó tổng các phẩn tử của S là: -30 + 34 = 4.