Cho số phức z thỏa điều kiện trị tuyệt đối của (z+2)

* Hướng dẫn giải

Đáp án D

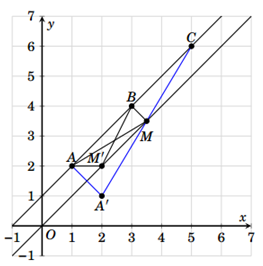
Cách 1

·       Đặt   biểu diễn cho số phức z.

·       Từ giả thiết, ta có M  thuộc đường trung trực  của đoạn EF và P=AM+BM+CM 

·       Ta chứng minh điểm M chính là hình chiếu vuông góc của B lên đường thẳng $∆$ .

-        Với M’ tùy ý thuộc$∆$, M’ khác M. Gọi  A’ là điểm đối xứng của A qua $∆$. Nhận thấy rằng ba điểm A’, M, C thẳng hàng.

-        Ta có  

Mà  

Lại có  Do đó  

Cách 2

·       Gọi  Từ giả thiết  , dẫn đến y=x .

Khi đó z=x+xi. 

·        

·       Sử dụng bất đẳng thức  

Dấu đẳng thức xảy ra khi và chỉ khi  . Ta có

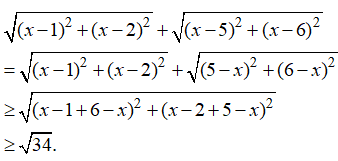
Dấu đẳng thức xảy ra khi và chỉ khi  

·       Mặt khác

Dấu đẳng thức xảy ra khi và chỉ khi x= $\frac{7}{2}$ 

·       Từ hai trường hợp trên, ta thấy, giá trị nhỏ nhất của P là  .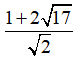

Khi đó  a+b=3.