Cho số phức z thỏa mãn môđun của (z-2-3i)=1 Giá trị lớn nhất

* Hướng dẫn giải

Đáp án D.

Gọi z=x+yi ta có z-2-3i=x+yi-2-3i=x-2+(y-3)i.

Theo giả thiết  nên  điểm M biểu diễn cho số phức z nằm trên đường tròn tâm I(2;3) bán kính R=1.

Ta có

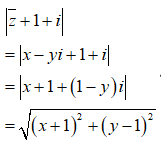
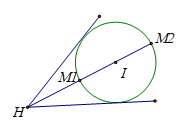
Gọi M(x;y) và H(-1;1) thì 

Do M chạy trên đường tròn, H cố định nên MH lớn nhất khi M là giao của HI với đường tròn.

Phương trình 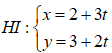, giao HI và đường tròn ứng với t thỏa mãn:

nên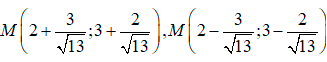 

Tính độ dài MH ta lấy kết quả HM=$\sqrt{13}+1$.