Gọi M là trung điểm của \(AA_1\). Thể tích khối chóp \(M.BC{A_1}\)

* Hướng dẫn giải

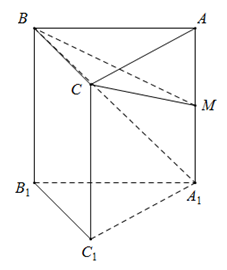
\(\Delta ABC\)là tam giác đều cạnh \(a\)nên có diện tích \({S_{ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\)

Ta có \(AM = \dfrac{{A{A_1}}}{2} = \dfrac{a}{2}\)

Hai tứ diện \(MABC\)và \(M{A_1}BC\)có chung đỉnh\(C\), diện tích hai đáy \(MAB\)và \(M{A_1}B\)bằng nhau nên có thể tích bằng nhau, suy ra

\({V_{M.BC{A_1}}} = {V_{M.ABC}} = \dfrac{1}{3}AM.{S_{ABC}} \)\(\,= \dfrac{{{a^3}\sqrt 3 }}{{24}}\)