Đề thi giữa HK1 môn Toán 12 năm 2020 trường THPT Nguyễn Trung Trực
Câu 1 :
Hàm số \(y = - {x^3} + 3{x^2} - 4\) có đồ thị như hình vẽ sau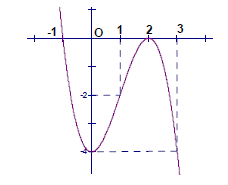
A. m = 0; m = 4.
B. m = - 4; m= 4.
C. m= - 4; m = 0
D. 0 < m < 4
Câu 2 : Điểm cực đại của hàm số \(y = - {x^3} + 3{x^2} + 2\)
A. x = 0
B. x = 2
C. (0 ; 2)
D. (2 ; 6)
Câu 3 : Tìm số giao điểm của đồ thị hàm số \(y = {x^4} - 3{x^2} - 5\) và trục hoành.
A. 4
B. 3
C. 1
D. 2
Câu 4 : Cho hàm số \(y = {x^3} - 2x + 1\) có đồ thị (C). Hệ số góc tiếp tuyến với (C) tại điểm M(- 1 ; 2) bằng:
A. 3
B. -5
C. 25
D. 1
Câu 5 : Điều kiện của tham số m đề hàm số \(y = \dfrac{{ - {x^3}}}{ 3} + {x^2} + mx\) nghịch biến trên R là
A. m < - 1
B. \(m \ge - 1\)
C. \(m > - 1\)
D. \(m \le - 1\)
Câu 6 : Đồ thị hàm số \(y = \dfrac{{2x - 3} }{{x - 1}}\) có các đường tiệm cận đứng và tiệm cận ngang lần lượt là bao nhiêu?
A. x = 2 và y = 1
B. x = 1 và y = - 3
C. x = - 1 và y = 2
D. x = 1 và y= 2
Câu 7 : Cho hàm số \(y = {x^3} - 3x\). Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng \(( - \infty ; - 1)\) và nghịch biến trên khoảng \((1; + \infty )\).
B. Hàm số đồng biến trên khoảng \(( - \infty ; + \infty )\).
C. Hàm số nghịch biến trên khoảng \(( - \infty ; - 1)\) và đồng biến trên khoảng \((1; + \infty )\).
D. Hàm số nghịch biến trên khoảng (- 1 ;1).
Câu 8 :
Cho hàm số y = f(x) có bảng biến thiên như sau: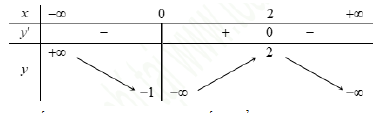
A. (-2; 1)
B. [-1 ; 2)
C. (-1 ; 2)
D. (- 2 ;1]
Câu 9 : Cho số dương a, biểu thức \(\sqrt a .\root 3 \of a \root 6 \of {{a^5}} \) viết dưới dạng lũy thừa hữu tỷ là:
A. \({a^{{5 \over 7}}}\)
B. \({a^{{1 \over 6}}}\)
C. \({a^{{7 \over 3}}}\)
D. \({a^{{5 \over 3}}}\)
Câu 10 : Tìm tập xác định của hàm số sau \(f(x) = \sqrt {{{\log }_2}{\dfrac{3 - 2x - {x^2}}{x + 1}}} \).
A. \(\left( { - \infty ;\dfrac{ - 3 - \sqrt {17} }{2}} \right] \cup \left( { - 1;\dfrac{ - 3 + \sqrt {17} }{2}} \right]\)
B. \(( - \infty ; - 3] \cup [1; + \infty )\).
C. \(\left[ {\dfrac{ - 3 - \sqrt {17} }{2}; - 1} \right) \cup \left[ {\dfrac{ - 3 + \sqrt {17} }{2};1} \right)\)
D. \(( - \infty ; - 3) \cup ( - 1;1)\).
Câu 11 : Giá trị của \({\log _a}\left( {\dfrac{{a^2}\root 3 \of {{a^2}} \root 5 \of {{a^4}} }{{\root {15} \of {{a^7}} }}} \right)\) bằng:
A. 3
B. \(\dfrac{12}{5}\)
C. \(\dfrac{9}{5}\)
D. 2
Câu 12 : Cho \({4^x} + {4^{ - x}} = 23\). Khi đó biểu thức \(K = \dfrac{5 + {2^x} + {2^{ - x}}}{{1 - {2^x} - {2^{ - x}}}}\) có giá trị bằng:
A. \( - \dfrac{5}{2}\)
B. \( \dfrac{3}{2}\)
C. \( - \dfrac{2}{5}\)
D. \(2\)
Câu 13 : Giá trị của \({\log _{{a^5}}}a\,\,\,(a > 0,\,\,a \ne 1)\) bằng:
A. \(\dfrac{1}{5}\)
B. - 3
C. 3
D. \(\dfrac{1}{3}\).
Câu 14 : Giá trị nhỏ nhất của hàm số \(y = {e^{{x^2}}}\) là:
A. 1
B. - 1
C. e
D. 0
Câu 15 : Số nghiệm của phương trình \({\log _5}(5x) - {\log _{25}}(5x) - 3 = 0\) là:
A. 3
B. 4
C. 1
D. 2
Câu 16 : Phương trình \({\log _2}x + {\log _2}(x - 1) = 1\) có tập nghiệm là:
A. {-1 ; 2}
B. {1 ; 3}
C. {2}
D. {- 1}
Câu 17 : Cho hàm số \(y = {1 \over 2}{\tan ^2}x + \ln (\cos x)\). Đạo hàm y’ bằng:
A. \(y' = \tan x - \cot x\)
B. \(y' = {\tan ^3}x\)
C. \(y' = {\cot ^3}x\)
D. \(y' = \tan x + \cot x\)
Câu 18 : Cho hàm số \(y = (x + 1).{e^x}\). Tính S= y’ – y
A. \( - 2{e^x}\)
B. \(2{e^x}\)
C. \({e^x}\)
D. \(x{e^x}\)
Câu 19 : Số cạnh của một khối chóp tam giác là bao nhiêu?
A. 4
B. 7
C. 6
D. 5
Câu 20 : Khi tăng kích thước mỗi cạnh của khối hộp chữ nhật lên 5 lần thì thể tích khối hộp chữ nhật tăng bao nhiêu lần?
A. 125
B. 25
C. 15
D. 5
Câu 21 : Cho hình chóp S.ABCD có đáy là hình vuông cạnh a và SA vuông góc với (ABC). Tính khoảng cách từ trọng tâm G của tam giác SAB đến (SAC)?
A. \(\dfrac{{a\sqrt 3 }}{6}\).
B. \(\dfrac{{a\sqrt 2 }}{6}\)
C. \(\dfrac{{a\sqrt 3 }}{2}\)
D. \(\dfrac{a \sqrt 2}{4}\)
Câu 22 : Một chiếc xe ô tô có thùng đựng hàng hình hộp chữ nhật với kích thước 3 chiều lần lượt là 2m; 1,5m; 0,7m. Tính thể tích thùng đựng hàng của xe ôtô đó.
A. \(14{m^3}\)
B. \(4,2{m^3}\)
C. \(8{m^3}\)
D. \(2,1{m^3}\)
Câu 23 : Cho khối lăng trụ tam giác đều \(ABC.{A_1}{B_1}{C_1}\) có tất cả các cạnh bằng a. Gọi M là trung điểm của \(AA_1\). Thể tích khối chóp \(M.BC{A_1}\) là:
A. \(\dfrac{{{a^3}\sqrt 3 }}{{12}}\)
B. \(\dfrac{{{a^3}\sqrt 3 }}{{24}}\)
C. \(dfrac{{{a^3}\sqrt 3 }}{6}\)
D. \(\dfrac{{{a^3}\sqrt 3 }}{8}\)
Câu 24 : Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a, cạnh \(SA = SB = SC = \dfrac{{a\sqrt 6 }}{3}\). Tính thể tích V của khối chóp đã cho.
A. \(V = \dfrac{{{a^3}}}{{12}}\)
B. \(V = \dfrac{{{a^3}\sqrt 2 }}{{12}}\)
C. \(V = \dfrac{{{a^3}}}{2}\)
D. \(V = \dfrac{{{a^3}\sqrt 3 }}{6}\)
Câu 25 : Công thức tính thể tích của khối lăng trụ có diện tích đáy B và chiều cao h
A. \(V = \dfrac{4}{3}Bh\)
B. \(V = \dfrac{1}{3}Bh.\)
C. \(V = \dfrac{1}{2}Bh\)
D. \(V = Bh.\)
Câu 26 : Cho lăng trụ tam giác ABC.A’B’C’ có thể tích là V, khi đó thể tích của khối chóp A’.ABC là
A. \(\dfrac{V}{3}\)
B. \(\dfrac{V}{4}\)
C. \(\dfrac{V}{6}\)
D. \(\dfrac{V}{2}\)
Câu 27 : Khối lập phương là khối đa diện đều loại
A. {5;3}
B. {3;4}
C. {4;3}
D. {3;5}
Lời giải có ở chi tiết câu hỏi nhé! (click chuột vào câu hỏi).
Copyright © 2021 HOCTAP247
