Hàm số \(y = {x^3} - 3{x^2} + 3x - 4\) có bao nhiêu cực trị?

* Hướng dẫn giải

\(y = {x^3} - 3{x^2} + 3x - 4\)

TXD:D = R

\(\begin{array}{l}y' = 3{x^2} - 6x + 3\\y' = 0 \Leftrightarrow 3{x^2} - 6x + 3 = 0\\ \Leftrightarrow x = 1\end{array}\)

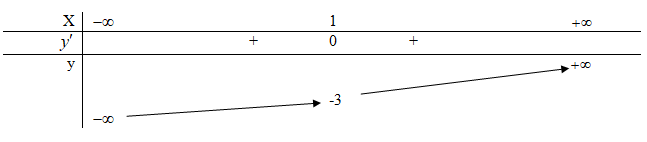
Hàm số đồng biến trên R nên không có cực trị.