Giá trị nhỏ nhất của hàm số \(y = \sin x - \frac{4}{3}{\sin ^3}x\) trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \r

* Hướng dẫn giải

Đặt t=sinx
Do \(x \in \left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) nên \(t \in \left( { - 1;1} \right)\)
Xét hàm số: \(f(t) = t - \frac{4}{3}{t^3},t \in \left( { - 1;1} \right)\)
\(y' = 1 - 4{t^2}\\ y' = 0 \Leftrightarrow \left[ \begin{array}{l} t = \frac{1}{2}\\ t = - \frac{1}{2} \end{array} \right.\)
Bảng biến thiên:

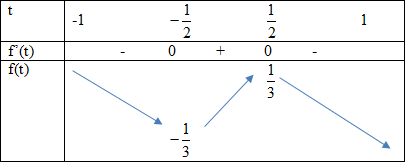
Vậy
\(\mathop {\min }\limits_{t \in \left[ { - 1;1} \right]} f(t) = - \frac{1}{3}\)