20 câu Trắc nghiệm Online Đạo hàm và ứng dụng Toán 12 có video giải năm học 2016 - 2017
Câu 1 : Trong các phát biểu sau, phát biểu nào đúng?
A. Hàm số f(x) nghịch biến trên (a;b) khi và chỉ khi \(f'(x)\leq 0 \ \forall x\in (a;b)\)
B. Nếu \(f'(x)\leq 0 \ \forall x\in (a;b)\) thì hàm số f(x) nghịch biến trên (a;b)
C. Hàm số y= f(x) nghịch biến trên (a;b) khi và chỉ khi \(f'(x)< 0 \ \forall x\in (a;b)\)
D. Nếu \(f'(x)< 0 \ \forall x\in (a;b)\) thì hàm số y = f(x) nghịch biến trên (a;b)
Câu 2 :
Cho hàm số có bảng biến thiên sau: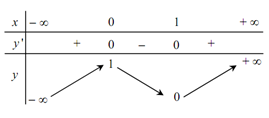
Phát biểu nào sau đây là đúng.
A. Hàm số đồng biến trên\(( - \infty ;0) \cup \left( {1; + \infty } \right)\) và nghịch biến trên (0;1)
B. Hàm số đồng biến trên hai khoảng \(( - \infty ;1);\left( {0; + \infty } \right)\) và nghịch biến trên (0;1)
C. Hàm số đồng biến trên hai khoảng \((- \infty ;0);\left( {1; + \infty } \right)\) và nghịch biến trên (0; 1)
D. Hàm số đồng biến trên \(\mathbb{R} \setminus \left( {0;1} \right)\) và nghịch biến trên (0; 1)
Câu 3 :
Cho hàm số có bảng biến thiên sau:
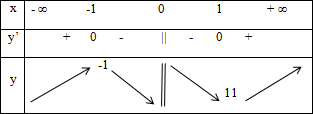
Phát biểu nào sau đây là đúng.
A. Hàm số đồng biến trên hai khoảng \(( - \infty ; - 1);\left( {11; + \infty } \right)\) và nghịch biến trên (-1; 11)
B. Hàm số đồng biến trên hai khoảng \(( - \infty ; - 1);\left( {1; + \infty } \right)\) và nghịch biến trên (-1; 0); (0; 1)
C. Hàm số đồng biến trên hai khoảng \(( - \infty ; - 1);\left( {1; + \infty } \right)\) và nghịch biến trên (-1; 1)
D. Hàm số đồng biến trên hai khoảng \(( - \infty ; - 1) \cup \left( {1; + \infty } \right)\) và nghịch biến trên (-1; 0); (0; 1)
Câu 4 : Hàm số f(x) có đạo hàm \(f'(x) = {x^2}(x + 2)\) Phát biểu nào sau đây là đúng?
A. Hàm số đồng biến trên khoảng \(\left( { - \infty ; - 2} \right);\left( {0; + \infty } \right)\)
B. Hàm số đồng biến trên khoảng (-2; 0)
C. Hàm số nghịch biến trên khoảng \(\left( { - \infty ; - 2} \right);\left( {0; + \infty } \right)\)
D. Hàm số đồng biến trên khoảng \((-2 ;+\infty )\)
Câu 5 : Hàm số \(y = - {x^3} - 3{x^2} - 4\) đồng biến trên khoảng nào sau đây:
A. (-2;0)
B. (-3;0)
C. \((-\infty ;-2)\)
D. \((0;+\infty )\)
Câu 6 : Cho hàm số \(y = \frac{{mx - 3}}{{x + 1}}\). Tập hợp giá trị m để hàm số đồng biến trên từng khoảng xác định là:
A. \(\mathbb{R}\setminus {-3}\)
B. \((-3;+\infty )\)
C. \((-\infty ;-3)\)
D. \(\left \{ 3 \right \}\)
Câu 7 : Hàm số f(x) có đạo hàm \(f'(x) = {x^2}{(x + 1)^2}\). Số cực trị của hàm số là
A. 1
B. 2
C. 0
D. 3
Câu 8 : Hàm số f(x) có đạo hàm \(f'(x) = {x^2}{(x + 1)^2}(x + 2).\) Phát biểu nào sau đây là đúng:
A. Hàm số đạt cực tiểu tại x = -2
B. Hàm số đạt cực tiểu tại x = -2, x = 0. Hàm số đạt cực đại tại x = - 1
C. Hàm số đạt cực đại tại x = -2, x = 0 Hàm số đạt cực tiểu tại x =-1
D. Hàm số không có cực trị.
Câu 9 : Giá trị cực đại của hàm số \(y = {x^3} - 3x + 2\) là:
A. -1
B. 1
C. 0
D. 4
Câu 10 :
Cho hàm số có bảng biến thiên dưới đây. Phát biểu nào là đúng?
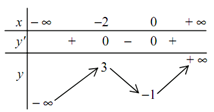
A. Hàm số đạt cực tiểu tại x = -1 và đạt cực đại tại x = 3
B. Giá trị cực tiểu của hàm số là 0
C. Giá trị cực đại của hàm số là -2
D. Hàm số đạt cực đại tại x = -2 và đạt cực tiểu tại x = 0
Câu 11 : Điểm cực đại của đồ thị hàm số \(y = \frac{1}{2}{x^4} - 2{x^2} - 3\) là:
A. (0;-3)
B. 0
C. \((\sqrt{-2};-5);(\sqrt{2};-5)\)
D. -3
Câu 12 :
Cho hàm số có bảng biến thiên sau
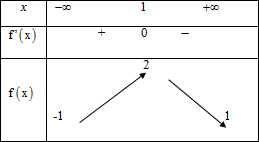
Trong các khẳng định sau khẳng định nào đúng?
A. Đồ thị hàm số có hai tiệm cận ngang là y=-1, y=1
B. Đồ thị hàm số có hai tiệm cận ngang là x=-1,x=1
C. Đồ thị hàm số không có tiệm cận ngang.
D. Đồ thị hàm số có có tiệm cận đứng.
Câu 13 : Cho hàm số \(y = \frac{{x + 1}}{{\sqrt {{x^2} - 1} }}.\) Số tiệm cận ngang của đồ thị hàm số là:
A. 1
B. 2
C. 0
D. Không thể xác định được
Câu 14 : Cho hàm số \(y = \frac{{2x - 3}}{{x + 1}}\). Giao điểm hai đường tiệm cận của đồ thị hàm số có tọa độ là:
A. (-1;2)
B. \((\frac{3}{2};2)\)
C. (2; -1)
D. \((-1;\frac{3}{2})\)
Câu 15 : Cho hàm số \(y = {x^3} + 5x + 7.\) Giá trị lớn nhất của hàm số trên đoạn [-5; 0] là:
A. 7
B. -143
C. 6
D. 8
Câu 16 :
Cho hàm số có bảng biến thiên sau
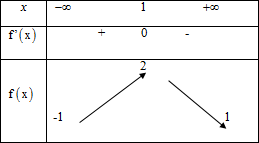
Trong các khẳng định sau khẳng định nào đúng?
A. Giá trị lớn nhất của hàm số là 2.
B. Giá trị nhỏ nhất của hàm số là -1
C. Giá trị nhỏ nhất của hàm số là -1 và 1
D. Giá trị lớn nhất của hàm số là 1
Câu 17 : Giá trị nhỏ nhất của hàm số \(y = \sin x - \frac{4}{3}{\sin ^3}x\) trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) bằng:
A. \(-\frac{1}{3}\)
B. 1
C. \(\frac{1}{3}\)
D. -3
Câu 18 : Cho biểu thức \(A = \frac{{2xy}}{{{x^2} + {y^2}}},\) với \(x, y\neq 0\) Giá trị nhỏ nhất của A bằng:
A. 1
B. 0
C. -1
D. Không có giá trị nhỏ nhất
Câu 19 : Một công ty muốn thiết kế một loại hộp có dạng hình hộp chữ nhật, đáy là hình vuông và thể tích khối hộp được tạo thành là 8 dm3 Độ dài cạnh đáy của mỗi hộp muốn thiết kế để diện tích toàn phần đạt giá trị nhỏ nhất là:
A. \(2\sqrt[3]{2}\)
B. 2
C. 4
D. Không có giá trị nhỏ nhất
Lời giải có ở chi tiết câu hỏi nhé! (click chuột vào câu hỏi).
Copyright © 2021 HOCTAP247
