Một công ty muốn thiết kế một loại hộp có dạng hình hộp chữ nhật, đáy là hình vuông và thể tích khối hộp đượ

* Hướng dẫn giải

Gọi độ dài cạnh đáy là x.

Độ dài đường cao là y.

Thể tích khối hộp là: V=x²y = 8 (1)

Diện tích toàn phần: S=2x² + 4xy (2)

Bài toàn trở thành tìm x,y sao cho S đạt GTNN.
Từ (1) suy ra: \(y = \frac{8}{{{x^2}}}\) thay vào (2) ta có:
\(S = 2{x^2} + 4x\frac{8}{{{x^2}}} = 2{x^2} + \frac{{32}}{x}\)
Xét hàm số: 
\(f(x) = 2{x^2} + \frac{{32}}{x}\,;x \in \left( {0; + \infty } \right)\)
Ta có: 
\(f'(x) = 4x - \frac{{32}}{{{x^2}}}\\ f'(x) = 0 \Leftrightarrow 4x = \frac{{32}}{{{x^2}}} \Leftrightarrow 4{x^3} - 32 = 0 \Leftrightarrow x = 2\)
Bảng Biến thiên:

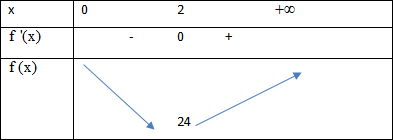
Vậy \(\mathop {\min }\limits_{x \in \left( {0; + \infty } \right)} f(x) = 24\)  tại x=2.
Vậy diện tích xung quanh đạt GTNN khi độ dài cạnh đáy bằng 2.