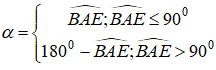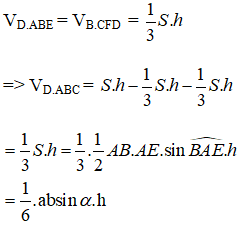Trang chủ
Đề thi & kiểm tra
Lớp 12
Toán học
Giải bài tập Hình học 12 !!
Cho hai đường thẳng chéo nhau d và d’. Đoạn...
Cho hai đường thẳng chéo nhau d và d’. Đoạn thẳng AB có độ dài bằng a trượt trên d
Câu hỏi :
Cho hai đường thẳng chéo nhau d và d’. Đoạn thẳng AB có độ dài bằng a trượt trên d, đoạn thẳng CD có độ dài bằng b trượt trên d’. Chứng minh rằng khối tứ diện ABCD có thể tích không đổi.
* Đáp án
* Hướng dẫn giải
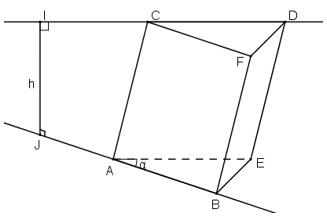
Gọi h là khoảng cách hai đường thẳng d và d’, gọi α là góc tạo bởi hai đường thẳng d và d’.
Lần lượt vẽ hai hình bình hành BACF và ACDE.
Khi đó, ABE.CFD là hình lăng trụ tam tam giác có chiều cao h; AE = CD = b và
Gọi S là diện tích đáy của hình lăng trụ .
Ta chia hình lăng trụ ABE. CFD thành ba hình chóp tam giác là: D. ABE, B. CFD, D.ABC. Ta có:
Do đó, thể tích khối tứ diện ABCD không đổi.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải bài tập Hình học 12 !!
Số câu hỏi: 202
Copyright © 2021 HOCTAP247