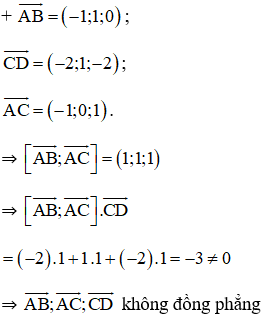Trang chủ
Đề thi & kiểm tra
Lớp 12
Toán học
Giải bài tập Hình học 12 !!
Cho bốn điểm A(1; 0; 0), B(0; 1; 0), C(0;...
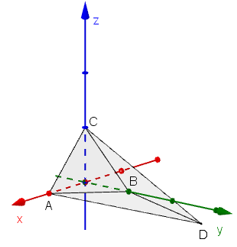
Cho bốn điểm A(1; 0; 0), B(0; 1; 0), C(0; 0; 1), D(-2; 1; -1) Chứng minh A, B, C, D là bốn đỉnh của một tứ diện
Câu hỏi :
Cho bốn điểm A(1; 0; 0), B(0; 1; 0), C(0; 0; 1), D(-2; 1; -1) Chứng minh A, B, C, D là bốn đỉnh của một tứ diện.
* Đáp án
* Hướng dẫn giải
a) Cách 1:
Phương trình đoạn chắn (ABC) là:
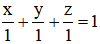
Thay tọa độ điểm D(-2; 1; -1) ta được: (-2) + 1 + (-1) – 1 = -3 ≠ 0
⇒ D không nằm trong (ABC)
⇒ A, B, C, D không đồng phẳng
⇒ A, B, C, D là bốn đỉnh của một tứ diện.
Cách 2:
⇒ A, B, C, D không đồng phẳng
⇒ A, B, C, D là bốn đỉnh của hình tứ diện.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải bài tập Hình học 12 !!
Số câu hỏi: 202
Copyright © 2021 HOCTAP247