Cho mặt cầu(S) có phương trình (x – 3)^2 + (y + 2)^2 + (z – 1)^2 = 100

* Hướng dẫn giải

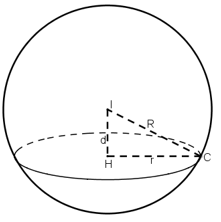
Từ phương trình ${\left(x-3\right)}^2+{\left(y+2\right)}^2+{\left(z-1\right)}^2=100$ ta suy ra mặt cầu (S) có tâm I(3;-2;1) và có bán kính R=10. Gọi H là tâm cả đường tròn (C) - Hình chiếu vuông góc của I trên mặt phẳng ($\alpha$)

Phương trình tham số của đường thẳng IH là: $\left\{\begin{array}{l}x=3+2t\\ y=-2-2t\\ z=1-t\end{array}\right.$ Thay x,y,z từ phương trình tham số của đường thẳng IH vào phương trình mp $\left(\alpha \right)$ tại H(-1;2;3). H là tâm của đường tròn (C). Vậy bán kính của đường tròn (C) là