Trang chủ
Đề thi & kiểm tra
Lớp 12
Toán học
Thi Online Đề thi THPT QG 2018 môn Toán - Mã đề 101 có video HD giải
Câu 50 mã đề 101 Cho hình nón đỉnh S...
Câu 50 mã đề 101 Cho hình nón đỉnh S có chiều cao h=a và bán kính đáy r=2a
Câu hỏi :
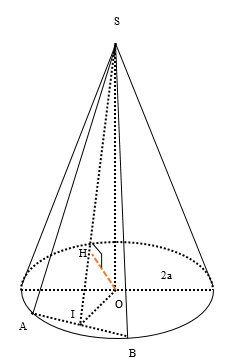
Cho hình nón đỉnh S có chiều cao \(h = a\) và bán kính đáy \(r = 2a\) . Mặt phẳng (P) đi qua S cắt đường tròn đáy tại A và B sao cho \(AB = 2\sqrt 3 a\) . Tính khoảng cách d từ tâm của đường tròn đáy đến (P) .
A. \(d = \frac{{\sqrt 3 a}}{2}\)
B. \(d = a\)
C. \(d = \frac{{\sqrt 5 a}}{5}\)
D. \(d = \frac{{\sqrt 2 a}}{2}\)
* Đáp án
D
* Hướng dẫn giải
Gọi O là tâm của đáy, I là trung điểm của AB
Ta có: \(\begin{array}{l}\left\{ \begin{array}{l}(SOI) \bot (SAB)\\(SOI) \cap (SAB) = SI\end{array} \right.\\\end{array}\)
\( \Rightarrow \) Trong (SOI), kẻ \(OH \bot SI,(H \in SI)\)
Thì \(OH \bot (SAB) \Rightarrow OH = d(O,(SAB)) = d(O,(P))\)
Xét \(\Delta OIB\) vuông tại I:
\(OI = \sqrt {O{B^2} - B{I^2}} = a\)
Xét \(\Delta SOI\) vuông tại O:
\(\frac{1}{{O{H^2}}} = \frac{1}{{S{O^2}}} + \frac{1}{{O{I^2}}} = \frac{2}{{{a^2}}} \Rightarrow OH = \frac{{a\sqrt 2 }}{2} = d(O,(P)).\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Thi Online Đề thi THPT QG 2018 môn Toán - Mã đề 101 có video HD giải
Số câu hỏi: 50
Copyright © 2021 HOCTAP247