Cho hàm số y = -x^3 + 3x^2 + 3mx - 1, tìm tất cả các giá trị của tham số m để

* Hướng dẫn giải

Ta có $y\text{'}=-3x^2+6x+3m$. Hàm số nghịch biến trên khoảng (0; +∞) nếu y' ≤ 0 trên khoảng (o; +∞)

Cách 1: Dùng định lí dấu tam thức bậc hai.

Xét phương trình $-3x^2+6x+3m$. Ta có Δ' = 9(1 + m)

TH1: Δ' ≤ 0 => m ≤ -1 khi đó, $-3x^2+6x+3m<0$ nên hàm số nghịch biến trên R .

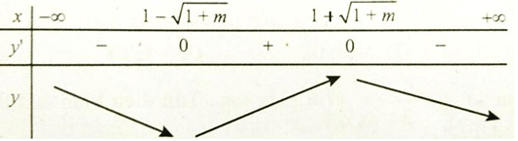
TH2: Δ' > 0 => m > -1; y' = 0 có hai nghiệm phân biệt là x = 1 ±√(1+m) .

Hàm số nghịch biến trên (0; +∞) <=> 1 + √(1+m) ≤ 0, vô lí.

Từ TH1 và TH2, ta có m ≤ -1

Cách 2: Dùng phương pháp biến thiên hàm số (cô lập tham số m).

Ta có: $y\text{'} = -3x^2 + 6x + 3m \le 0$, ∀x > 0 <=>$3m \le 3x^2 - 6x$, ∀x > 0

Từ đó suy ra $3m \le min(3x^2 - 6x)$ với x > 0

Mà $3x^2-6x=3(x^2-2x+1)-3=3(x-1{)}^2-3\ge -3\forall x$

Suy ra: $min( 3x^2 – 6x) = - 3$ khi x= 1

Do đó 3m ≤ -3 hay m ≤ -1.

Chọn đáp án C.