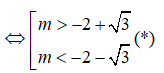Trang chủ
Đề thi & kiểm tra
Lớp 12
Toán học
28 câu trắc nghiệm: Cực trị của hàm số có đáp án !!
Với giá trị nào của m, hàm số y =...
Với giá trị nào của m, hàm số y = x^3 + 2(m - 1)x^2 + (m^2 - 4m + 1)x + 2(m^2 + 1)
Câu hỏi :
Với giá trị nào của m, hàm số có hai điểm cực trị thỏa mãn
A. m = 5 hoặc m = 1
B. m = 2 hoặc m = 1
C. m = 5
D. m = 1
* Đáp án
A
* Hướng dẫn giải
Chọn A
Ta có Hàm số có hai cực trị
=> y' = 0 có hai nghiệm phân biệt <=> Δ' > 0 <=>
<=>
Áp dụng Vi-ét cho phương trình y’ = 0 có hai nghiệm phân biệt ta có
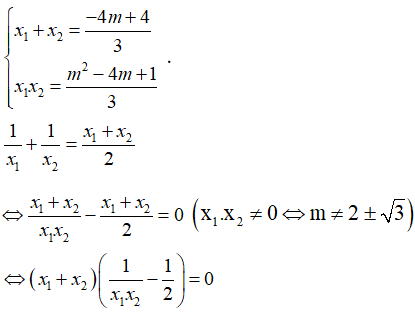
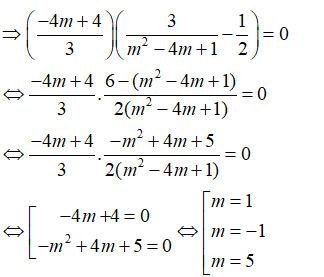
Đối chiếu điều kiện có m = 5 hoặc m = 1
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
28 câu trắc nghiệm: Cực trị của hàm số có đáp án !!
Số câu hỏi: 28
Copyright © 2021 HOCTAP247