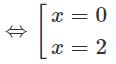Trang chủ
Đề thi & kiểm tra
Lớp 12
Toán học
Giải SBT Toán 12 Bài 3: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số !!
Tìm các giá trị của m để phương trình :...
Tìm các giá trị của m để phương trình : x^3 – 3x^2 – m = 0 có ba
Câu hỏi :
Tìm các giá trị của m để phương trình : – 3 – m = 0 có ba nghiệm phân biệt.
* Đáp án
* Hướng dẫn giải
Đặt f(x) = – 3 (C1)
y = m ()
Phương trình – 3 – m = 0 có ba nghiệm phân biệt khi và chỉ khi () và () có ba giao điểm.
Ta có:
f′(x) = 3 − 6x = 3x(x − 2) = 0
Bảng biến thiên:
Suy ra () và () cắt nhau tại 3 điểm khi -4 < m < 0
Kết luận : Phương trình – 3 – m = 0 có ba nghiệm phân biệt với những giá trị của m thỏa mãn điều kiện: -4 < m < 0.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải SBT Toán 12 Bài 3: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số !!
Số câu hỏi: 17
Copyright © 2021 HOCTAP247