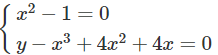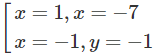Trang chủ
Đề thi & kiểm tra
Lớp 12
Toán học
Giải SBT Toán 12 Bài 5: Khảo sát sự biến thiên và vẽ đồ thị của hàm số !!
Cho hàm số: y = x^3 − (m + 4)x^2...
Cho hàm số: y = x^3 − (m + 4)x^2 − 4x + m (1). Tìm các điểm mà đồ thị
Câu hỏi :
Cho hàm số: y = − (m + 4) − 4x + m (1). Tìm các điểm mà đồ thị của hàm số (1) đi qua với mọi giá trị của m
* Đáp án
* Hướng dẫn giải
y = − (m + 4) − 4x + m
⇔ ( − 1)m + y − + 4 + 4x = 0
Đồ thị của hàm số (1) luôn luôn đi qua điểm A(x; y) với mọi m khi (x; y) là nghiệm của hệ phương trình:
Giải hệ, ta được hai nghiệm:
Vậy đồ thị của hàm số luôn luôn đi qua hai điểm (1; -7) và (-1; -1).
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải SBT Toán 12 Bài 5: Khảo sát sự biến thiên và vẽ đồ thị của hàm số !!
Số câu hỏi: 30
Copyright © 2021 HOCTAP247