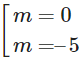Trang chủ
Đề thi & kiểm tra
Lớp 12
Toán học
Giải SBT Toán 12 Bài tập ôn tập chương 1 !!
Cho hàm số: y = –(m^2 + 5m)x^3 + 6mx^2...
Cho hàm số: y = –(m^2 + 5m)x^3 + 6mx^2 + 6x – 5. Xác định m để hàm số
Câu hỏi :
Cho hàm số: y = –( + 5m) + 6m + 6x – 5. Xác định m để hàm số đơn điệu trên R. Khi đó, hàm số đồng biến hay nghịch biến? Tại sao?
* Đáp án
* Hướng dẫn giải
y = –( + 5m) + 6m + 6x – 5
y′ = –3( + 5m) + 12mx + 6
Hàm số đơn điệu trên R khi và chỉ khi y’ không đổi dấu.
Ta xét các trường hợp:
+) + 5m = 0 ⇔
– Với m = 0 thì y’ = 6 nên hàm số luôn đồng biến.
– Với m = -5 thì y’ = -60x + 6 đổi dấu khi x đi qua .
+) Với + 5m 0. Khi đó, y’ không đổi dấu nếu
' = 36 + 18( + 5m) 0 ⇔ 3 + 5m 0 ⇔ –5/3 m 0
– Với điều kiện đó, ta có –3( + 5m) > 0 nên y’ > 0 và do đó hàm số đồng biến trên R.
Vậy với điều kiện –5/3 m 0 thì hàm số đồng biến trên R.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải SBT Toán 12 Bài tập ôn tập chương 1 !!
Số câu hỏi: 31
Copyright © 2021 HOCTAP247