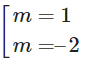Trang chủ
Đề thi & kiểm tra
Lớp 12
Toán học
Giải SBT Toán 12 Bài tập ôn tập chương 1 !!
Cho hàm số: y = –(m^2 + 5m)x^3 + 6mx^2...
Cho hàm số: y = –(m^2 + 5m)x^3 + 6mx^2 + 6x – 5. Với giá trị nào của m thì
Câu hỏi :
Cho hàm số: y = –( + 5m) + 6m + 6x – 5. Với giá trị nào của m thì hàm số đạt cực đại tại x = 1 ?
* Đáp án
* Hướng dẫn giải
Nếu hàm số đạt cực đại tại x = 1 thì y’(1) = 0. Khi đó:
y′(1) = –3 – 3m + 6 = 0 ⇔
Mặt khác, y” = –6( + 5m)x + 12m
+) Với m = 1 thì y’’ = -36x + 12. Khi đó, y’’(1) = -24 < 0 , hàm số đạt cực đại tại x = 1.
+) Với m = -2 thì y’’ = 36x – 24. Khi đó, y’’(1) = 12 > 0, hàm số đạt cực tiểu tại x = 1.
Vậy với m = 1 thì hàm số đạt cực đại tại x = 1.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải SBT Toán 12 Bài tập ôn tập chương 1 !!
Số câu hỏi: 31
Copyright © 2021 HOCTAP247