Cho hàm số y=f(x) có bảng biến thiên như sau: Số nghiệm thuộc đoạn \(\left[ -\pi ;\pi \right]\) của phương trình \(3f(2\sin x)+1=0\) là
Câu hỏi :
Cho hàm số y=f(x) có bảng biến thiên như sau: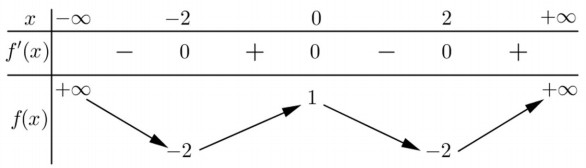
A. 4
B. 5
C. 2
D. 6
* Đáp án
A
* Hướng dẫn giải
Đặt \(t=2\sin x\). Vì \(x\in \left[ -\pi ;\pi \right]\) nên \(t\in \left[ -2;2 \right].\) Suy ra \(3f(t)+1=0\Leftrightarrow f(t)=-\frac{1}{3}.\)
Dựa vào bảng biến thiên, phương trình \(f(t)=-\frac{1}{3}\) có 2 nghiệm \({{t}_{1}}\in \left( -2;0 \right)$ và \({{t}_{2}}\in \left( 0;2 \right)\)
Suy ra: \(\operatorname{s}\text{inx}=\frac{{{t}_{1}}}{2}\in (-1;0)\) và \(\operatorname{s}\text{inx}=\frac{{{t}_{2}}}{2}\in (0;1).\)
Với \(\operatorname{s}\text{inx}=\frac{{{t}_{1}}}{2}\in (-1;0)\) thì phương trình có 2 nghiệm \(-\pi <{{x}_{1}}<{{x}_{2}}<0.\)
Với \(\operatorname{s}\text{inx}=\frac{{{t}_{2}}}{2}\in (0;1)\) thì phương trình có 2 nghiệm \(0<{{x}_{3}}<{{x}_{4}}<\pi .\)
Vậy phương trình có 4 nghiệm phân biệt thuộc đoạn \(\left[ -\pi ;\pi \right]\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Toán - Trường THPT Trà Bồng
Copyright © 2021 HOCTAP247
