Một sân chơi cho trẻ em hình chữ nhật có chiều dài 100 m và chiều rộng là 60 m người ta làm một con đường nằm trong sân (tham khảo hình bên). Biết rằng viền ngoài và viền trong của...
Câu hỏi :
Một sân chơi cho trẻ em hình chữ nhật có chiều dài 100 m và chiều rộng là 60 m người ta làm một con đường nằm trong sân (tham khảo hình bên). Biết rằng viền ngoài và viền trong của con đường là hai đường elip, elip của đường viền ngoài có trục lớn và trục bé lần lượt song song với các cạnh hình chữ nhật và chiều rộng của mặt đường là 2 m. Kinh phí cho mỗi m2 làm đường 600 000 đồng. Tính tổng số tiền (làm tròn đến hàng nghìn) làm con đường đó. 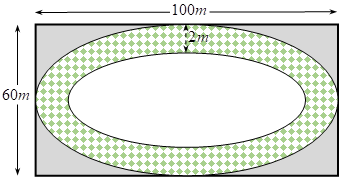
A. 294.053.000 đồng
B. 283.904.000 đồng
C. 293.804.000 đồng
D. 283.604.000 đồng
* Đáp án
A
* Hướng dẫn giải
Gắn hệ trục tọa độ Oxy: đặt gốc tọa độ O vào tâm của hình elip và hai trục tọa độ song song với các cạnh của hình chữ nhật.
+ Phương trình Elip của đường viền ngoài của con đường là \(\left( {{E}_{1}} \right):\frac{{{x}^{2}}}{{{50}^{2}}}+\frac{{{y}^{2}}}{{{30}^{2}}}=1\) Phần đồ thị của \(\left( {{E}_{1}} \right)\) nằm phía trên trục hoành có phương trình \(y=30\sqrt{1-\frac{{{x}^{2}}}{{{50}^{2}}}}={{f}_{1}}\left( x \right)\).
+ Phương trình Elip của đường viền trong của con đường là \(\left( {{E}_{2}} \right):\frac{{{x}^{2}}}{{{48}^{2}}}+\frac{{{y}^{2}}}{{{28}^{2}}}=1\). Phần đồ thị của \(\left( {{E}_{2}} \right)\) nằm phía trên trục hoành có phương trình \(y=28\sqrt{1-\frac{{{x}^{2}}}{{{48}^{2}}}}={{f}_{2}}\left( x \right)\)
+Gọi \({{S}_{1}}\) là diện tích của \(\left( {{E}_{1}} \right)\) và \({{S}_{2}}\) là diện tích của \(\left( {{E}_{2}} \right).\)
Gọi S là diện tích con đường. Khi đó
\(S={{S}_{1}}-{{S}_{2}}=2\int\limits_{-50}^{50}{30\sqrt{1-\frac{{{x}^{2}}}{{{50}^{2}}}}\text{d}x}-2\int\limits_{-48}^{48}{28\sqrt{1-\frac{{{x}^{2}}}{{{48}^{2}}}}\text{d}x}\)
Tính tích phân \(I=2\int\limits_{-a}^{a}{b\sqrt{1-\frac{{{x}^{2}}}{{{a}^{2}}}}\text{d}x},\left( a,b\in {{\mathbb{R}}^{+}} \right)\)
Đặt \(x=a\sin t,\left( -\frac{\pi }{2}\le t\le \frac{\pi }{2} \right)\Rightarrow \text{d}x=a\cos t\text{d}t\).
Đổi cận \(x=-a\Rightarrow t=-\frac{\pi }{2};x=a\Rightarrow t=\frac{\pi }{2}.\)
Khi đó \(I=2\int\limits_{-\frac{\pi }{2}}^{\frac{\pi }{2}}{b\sqrt{1-{{\sin }^{2}}t}.a\cos t\,\text{d}t}=2ab\int\limits_{-\frac{\pi }{2}}^{\frac{\pi }{2}}{{{\cos }^{2}}t\,\text{d}t}=ab\int\limits_{-\frac{\pi }{2}}^{\frac{\pi }{2}}{\left( 1+\cos 2t \right)\text{d}t}\)
\(=ab\left. \left( t+\frac{\sin 2t}{2} \right) \right|_{-\frac{\pi }{2}}^{\frac{\pi }{2}}=ab\pi \)
Do đó \(S={{S}_{1}}-{{S}_{2}}=50.30\pi -48.28\pi =156\pi \)
Vậy tổng số tiền làm con đường đó là \(600000.S=600000.156\pi \approx 294053000\) đồng.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Toán - Trường THPT Thủ Đức lần 2
Copyright © 2021 HOCTAP247
