Cho mặt cầu tâm O bán kính r. Gọi (alpha) là mặt phẳng cách tâm O

Câu hỏi :

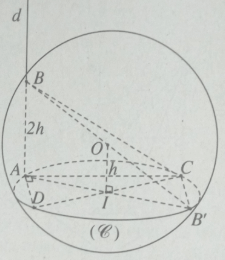
Cho mặt cầu tâm O bán kính r. Gọi ($\mathrm{\alpha }$) là mặt phẳng cách tâm O một khoảng h (0 < h < r) và cắt mặt cầu theo đường tròn (C). Đường thẳng d đi qua một điểm A cố định trên (C) và vuông góc với mặt phẳng ($\mathrm{\alpha }$) cắt mặt cầu tại một điểm B. Gọi CD là đường kính di động của (C). Chứng minh các tổng ${\mathrm{AD}}^2+{\mathrm{BC}}^2$ và ${\mathrm{AC}}^2+{\mathrm{BD}}^2$ có giá trị không đổi